Инварианты поля.
Рассмотрим для простоты случай, когда соответствующие оси ИСО s и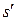 
взаимно параллельны, относительное движение происходит вдоль 
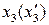, а в начальный момент время 
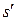начала обоих ИСО совпадают. Тогда компоненты тензора F при переходе от s к преобразуются по закону
, (1)
где
, 
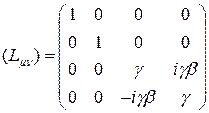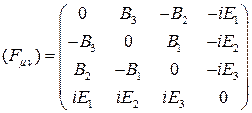
Получим:
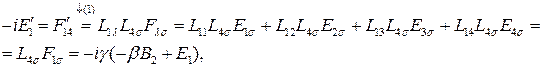
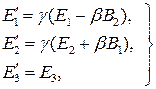(2)
(3)
Видно, что, что компоненты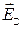 
и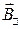 
, параллельные скорости относительного движения систем отсчета, не изменяются, а перпендикуллярные - 
и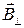 
- преобразуются в соответствии с полученными формулами. Разлагая E и B на продольную и поперечную составляющую
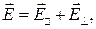
непосредственной проверкой убеждаемся, что:
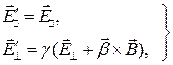(4)
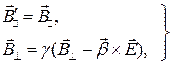. (5)
Найдём инварианты тензора 
.Ими являются, например, коэффициенты характеристического уравнения
.
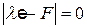В явном виде это уравнение 4-й степени относительно 
имеет вид:
. 
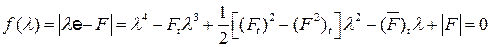Так как 
, то
.
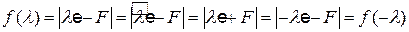Это означает, что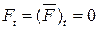 
и характеристическое уравнение примает вид
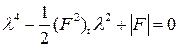. (7)
Найдем
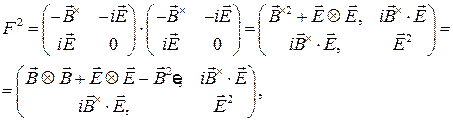
Здесь учтено, что 
, а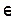 
- единичный оператор трехмерного.
Очевидно
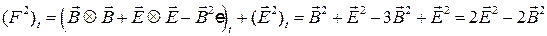
Следовательно, величина
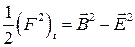(9)
- инвариант преобразований Лоренца.
Согласно теореме Гамильтона-Кэли любой тензор удовлетворяет своему характеристическому уравнению, т.е. имеет место соотношение
.
Отсюда следует, что оператор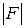 
можно вычислить следующим образом:
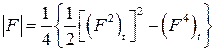. (10)
Найдем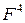 
:
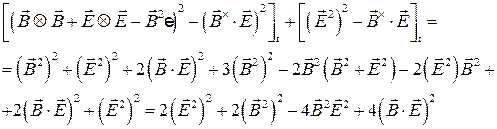
Таким образом, определитель 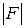равен
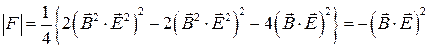. (11)
Значит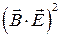 
- инвариант. Фактически, и величина 
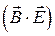является инвариантом преобразования Лоренца, но она допускает изменение знака.
Инварианты
, 
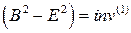(12)
отличаются тем, что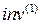 
- скаляр, а 
- псевдоскаляр. При отражении трёх пространственных осей или при инверсии времени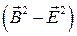 
не изменяется, а 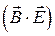меняет знак.
Из существования инвариантов электромагнитного поля вытекает ряд следствий. Пусть для простоты 
и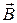 
вещественные векторы. Тогда
1. Если в некоторой ИСО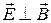 
, то и в любой другой ИСО 
.
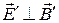2. Если в некоторой ИСО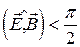 
, то и в любой другой ИСО 
.
3. Если в некоторой ИСО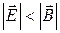 
, то и в любой другой ИСО 
.
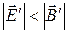4. Если в некоторой ИСО 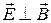и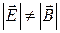 
, то существует такая ИСО, в которой любой из векторов поля или 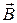равен нулю.
5. Если в некоторой ИСО 
, то и в любой другой ИСО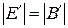 
.
6. Если в некоторой ИСО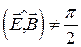 
, то существует такая ИСО, в которой 
.
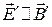Замечание: для поля в веществе, когда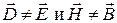 
, закон преобразования 
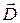и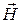 
получается из (4),(5) заменой 
и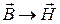 
.
Инвариантами поля наряду с (12), являются величины 
.
§5. Четырёхмерное обобщение силы Лоренца. Инвариантная форма записи законов сохранения.
Выпишем в явном виде её первую составляющую трёхмерной плотности силы Лоренца: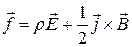 
- равна скорости изменения количества движения в единице объёма.
Запишем первую компоненту:
Аналогичного соотношения получаются и для 
, так что
(1)
Правые части (1) – представляют собой пространственные составляющие 4-вектора:
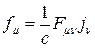(2)
который называют 4-вектора плотности силы Лоренца.
Выясним физический смысл четвертой составляющей вектора:
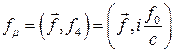
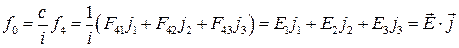(3)
Т.о.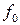 
– эта работа, совершаемая полем под зарядами в единичном объёме в единицу времени, т.е. скорость изменения механической энергии частицы в единице объёма. Пространственная же часть силы Лоренца определяет скорость изменения импульса в единице объёма. Законы сохранения полной энергии (механической и электромагнитной) и полного импульса можно представить в 4-х мерной инвариантной форме в виде уравнений для пространственной и временной части единого 4-вектора. А именно, из уравнений Максвелла:
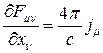(4)
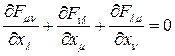(5)
Следует, что имеет место соотношение:
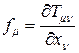(6)
где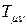 
- некоторый тензор второго ранга, называемый тензором энергии импульса.
Действительно, из (4) следует, что
Далее
(***) - проверяется непосредственно: 
Таким образом имеем:
Т.о. действительно имеет место (6), причём:
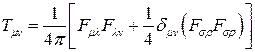(7)
В бескоординатном виде, очевидно
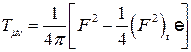(7)
Очевидно, что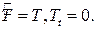 
Т.к.
, 
, то
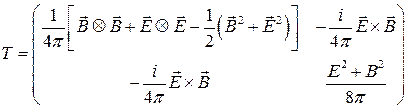(8)
Вспоминая определение тензора максвелловских натяжений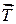 
, вектора Пойтинга 
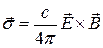и плотности импульса 
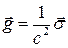, плотности
энергии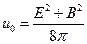 
, видим, что
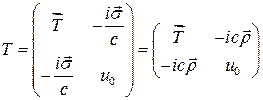(9)
Легко убедиться, что для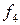 
из (6) следует
- закон сохранения энергии (в дифференциальной форме)
Аналогично (6) для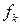 
приводит к соотношениям, выражающим закон сохранения импульса.
Инвариантность фазы плоской монохроматической волны.
