Закон Ома в дифференциальной форме описывает связь между векторами 
и 
. Пусть электрон движется в поле с напряженностью . По второму закону Ньютона, он приобретает ускорение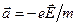 
, а его скорость возрастает по закону 
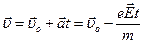, где 
- скорость электрона в отсутствии внешнего поля. При каждом столкновении происходит передача кинетической энергии электрона кристаллической решетке, и скорость падает почти до нуля. Усредним выражение для скорости в пределах среднего времени между столкновениями t
.
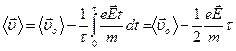Среднее значение скорости 
вследствие хаотичности скорости в отсутствие поля. Поэтому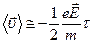 
. Учитывая определение 
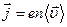(35), вектор плотности тока 
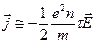. Произведение констант, стоящих перед , также является некоторой константой s, Þ
. (39)
Этот результат называется законом Ома в дифференциальной форме: плотность тока в каждой точке проводника пропорциональна напряженности поля в этой точке. Величина s называется проводимостью. Этот закон с высокой точностью выполняется только для металлов.
Часто закон Ома в дифференциальной форме записывают в виде
, (40)
где ρ – удельное сопротивление, которое возрастает с увеличением температуры t, oC по закону:
, (41)
где α – температурный коэффициент сопротивления; ρ о , a – табличные величины.
Закон Ома в интегральной форме. В простейшем случае для однородного участка цепи этот закон был установлен экспериментально
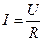. (42)
Величина R (сопротивление проводника) зависит от его формы, температуры и материала
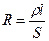, (43)
где l – длина, S – площадь поперечного сечения проводника. Единицей сопротивления является ом: [ R ]=[ Ом ]. Размерность удельного сопротивления [ ρ ]=[ Ом × м ].
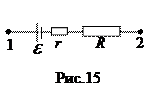
Рассмотрим неоднородный участок цепи, т.е. содержащий эдс. Реальный источник эдс можно рассматривать как идеальный, к которому последовательно присоединено его внутреннее сопротивление r (рис.15). Тогда U = I (R + r) ® (38), Þ
I (R + r)=(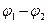
) + e. (44)
Это закон Ома в интегральной форме: Произведение силы тока в проводнике на сумму внешнего и внутреннего сопротивлений равно сумме разности потенциалов на концах проводника и действующей в проводнике эдс.
В замкнутой цепи точки 1 и 2 совпадают и 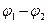=0, поэтому закон Ома принимает вид
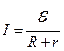. (45)
Когда цепь разомкнута, ток равен нулю, и тогда
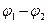| | = e. (46)
Эдсисточника равна разности потенциалов на его зажимах при разомкнутой цепи.
