В 1820 году Эрстед обнаружил, что магнитная стрелка устанавливается определенным образом по отношению к проводу, по которому идет ток. Это значит, что вокруг проводника с током существует магнитное поле, вызванное движением зарядов. Далее было установлено экспериментально, что магнитное поле действует на движущиеся заряды и не действует на покоящиеся.
Cила Лоренца. Опыт показывает, что сила, действующая на заряд q, зависит от его величины, положения и скорости. Эту силу разделяют на две составляющие – электрическую 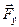 (не зависит от скорости заряда) и магнитную
(не зависит от скорости заряда) и магнитную  (она зависит от его скорости). Пусть магнитное поле описывается вектором магнитной индукции
(она зависит от его скорости). Пусть магнитное поле описывается вектором магнитной индукции  . Опыт показывает, что на заряд q, движущийся со скоростью
. Опыт показывает, что на заряд q, движущийся со скоростью  , действует магнитная сила
, действует магнитная сила
 =
=  , (50)
, (50)
по которой можно определить вектор  . На покоящийся заряд в магнитном поле сила не действует. Сила
. На покоящийся заряд в магнитном поле сила не действует. Сила  перпендикулярна вектору скорости заряда
перпендикулярна вектору скорости заряда  , поэтому она работы не совершает. Если есть еще и электрическое поле, то результирующая сила (она называется силой Лоренца) равна
, поэтому она работы не совершает. Если есть еще и электрическое поле, то результирующая сила (она называется силой Лоренца) равна

 . (51)
. (51)
Магнитное поле равномерно движущегося заряда. Опыт показывает, что точечный заряд q, движущийся со скоростью  , создает поле с магнитной индукцией
, создает поле с магнитной индукцией
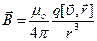 , (59)
, (59)
где магнитная постоянная  =4p×10-7 Гн/м;
=4p×10-7 Гн/м;  - радиус-вектор, проведенный от заряда q к точке наблюдения. Для магнитных полей, также как и для электрических, справедлив принцип суперпозиции.
- радиус-вектор, проведенный от заряда q к точке наблюдения. Для магнитных полей, также как и для электрических, справедлив принцип суперпозиции.
Теорема Гаусса для вектора  . Графически магнитное поле может быть представлено линиями вектора
. Графически магнитное поле может быть представлено линиями вектора  , касательная к которым в каждой точке совпадает с направлением вектора
, касательная к которым в каждой точке совпадает с направлением вектора  , а густота линий равна его модулю. Магнитное поле не имеет специальных магнитных источников, что и выражает теорема Гаусса для поля вектора
, а густота линий равна его модулю. Магнитное поле не имеет специальных магнитных источников, что и выражает теорема Гаусса для поля вектора  : Поток вектора
: Поток вектора  сквозь любую замкнутую поверхность равен нулю:
сквозь любую замкнутую поверхность равен нулю:
 . (63)
. (63)
Эта теорема выражает тот факт, что линии вектора  не имеют ни начала, ни конца. Поэтому число линий, выходящих из любого объема, ограниченного замкнутой поверхностью S, всегда равно числу линий, входящих в этот объем. Отсюда, поток вектора
не имеют ни начала, ни конца. Поэтому число линий, выходящих из любого объема, ограниченного замкнутой поверхностью S, всегда равно числу линий, входящих в этот объем. Отсюда, поток вектора  сквозь незамкнутую поверхность S, ограниченную некоторым замкнутым контуром, не зависит от формы этой поверхности.
сквозь незамкнутую поверхность S, ограниченную некоторым замкнутым контуром, не зависит от формы этой поверхности.
Теорема о циркуляции вектора  (для магнитного поля постоянных токов в вакууме). Циркуляция вектора
(для магнитного поля постоянных токов в вакууме). Циркуляция вектора  поля по произвольному замкнутому контуру Г равна произведению m о на алгебраическую сумму токов, охватываемых контуром Г:
поля по произвольному замкнутому контуру Г равна произведению m о на алгебраическую сумму токов, охватываемых контуром Г:
 = m о I, (64)
= m о I, (64)
 где
где  . Каждый ток в сумме – величина алгебраическая: ток считается >0, если направление движения положительных зарядов в нем связано с направлением обхода контура правилом правого винта.
. Каждый ток в сумме – величина алгебраическая: ток считается >0, если направление движения положительных зарядов в нем связано с направлением обхода контура правилом правого винта.
Так как правая часть выражения (64) не равна нулю, данное поле не потенциально. Подобные поля называют вихревыми, или соленоидальными. Теорема о циркуляции может быть применена для расчета поля вектора  . Сравним расчет магнитного поля прямого тока при помощи закона Био-Саварра с расчетом, в котором используется теорема о циркуляции вектора
. Сравним расчет магнитного поля прямого тока при помощи закона Био-Саварра с расчетом, в котором используется теорема о циркуляции вектора  .
.
Магнитное поле прямого тока. Рассмотрим бесконечный тонкий прямой проводник, по которому течет ток I (рис.18). В соответствии с (61) в произвольной точке А векторы  от всех элементов тока
от всех элементов тока  имеют одинаковое направление – за плоскость рисунка. Поэтому сложение векторов
имеют одинаковое направление – за плоскость рисунка. Поэтому сложение векторов  можно заменить сложением их модулей (удобнее в качестве угла α взять не угол между dl и r, а дополнительный к нему, поэтому вместо синуса - косинус)
можно заменить сложением их модулей (удобнее в качестве угла α взять не угол между dl и r, а дополнительный к нему, поэтому вместо синуса - косинус)
 .
.
Из рисунка 18 видно, что  и
и 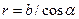 , Þ
, Þ
 .
.
Проинтегрируем это выражение в пределах изменения a от -p/ 2 до + p/ 2, Þ


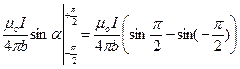 =
=  , Þ
, Þ
 . (65)
. (65)
Решим эту же задачу при помощи теоремы о циркуляции. Причем в данном случае откажемся от предположения о тонком проводнике. Пусть постоянный ток I течет вдоль бесконечного прямого провода, имеющего круглое сечение радиуса а, перпендикулярно рисунку 19. Найдем индукцию поля  снаружи и внутри провода. Из симметрии задачи следует, что силовые линии должны иметь вид перпендикулярных проводу окружностей с центром на оси провода. Причем модуль вектора
снаружи и внутри провода. Из симметрии задачи следует, что силовые линии должны иметь вид перпендикулярных проводу окружностей с центром на оси провода. Причем модуль вектора  должен быть одинаков для всех точек, расположенных на одинаковом расстоянии r от оси. Для контура Г 1 по теореме о циркуляции
должен быть одинаков для всех точек, расположенных на одинаковом расстоянии r от оси. Для контура Г 1 по теореме о циркуляции  , Þ
, Þ 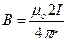 при (
при ( ), что по смыслу совпадает с (65); для контура Г 2:
), что по смыслу совпадает с (65); для контура Г 2:  , так как внутрь этого контура попадает только часть тока, пропорциональная отношению сечений. Þ
, так как внутрь этого контура попадает только часть тока, пропорциональная отношению сечений. Þ  при (
при ( ).
).






