Теорема о циркуляции вектора 
. В курсе механики было доказано, что работа поля центральных сил зависит только от начального и конечного положений частицы. Эквивалентным утверждением является: работа такого поля по перемещению частицы вдоль замкнутой траектории равна нулю. Такие поля называются потенциальными. Теорема о циркуляции вектора является выражением свойства потенциальности электростатического поля. Работа сил электростатического поля при перемещении точечного заряда q из точки 1 в точку 2 (рис.11):
.
Разделим эту работу на q:
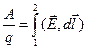. (17)
Отношение А/q это работа поля переноса единичного заряда из 1 в 2.
Интеграл вида (17), вычисленный вдоль замкнутой траектории, называется циркуляцией вектора :
.
Теорема о циркуляции вектора утверждает: циркуляция вектора напряженности электростатического поля по любому замкнутому контуру равна нулю: =0.
Доказательство. Электростатическое поле точечного заряда является полем центральных сил, и, следовательно, потенциальным. Поэтому работа его сил на замкнутом пути равна нулю: А = 
=0, Þ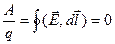 
. Таким образом, циркуляция поля точечного заряда равна нулю. Докажем это и для системы n точечных зарядов. По принципу суперпозиции напряженность поля системы точечных зарядов равна: 
. Умножим это равенство скалярно на вектор перемещения 
вдоль произвольного замкнутого контура и проинтегрируем по этому контуру:
. (18)
Каждый интеграл в правой части равен нулю как циркуляция вектора напряженности электростатического поля отдельного точечного заряда, следовательно, и вся сумма равна нулю. Таким образом, циркуляция электростатического поля системы n точечных зарядов также равна нулю. Переходя к пределу в (18) нетрудно убедиться, что и для непрерывно распределенного заряда циркуляция электростатического поля равна нулю.
