Индуктивность соленоида. При прохождении тока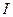 
по длинному соленоиду, внутри которого находится магнетик с магнитной проницаемостью m, в последнем возникает магнитное поле (60), равное 
. Пусть соленоид имеет площадь поперечного сечения S и полное число витков N. Тогда поток сквозь каждый виток Ф = ВS, а полный поток, сцепленный с соленоидом,
NФ = NВS = 
. Так как 
, где 
- число витков на единицу длины, 
- длина соленоида, то NФ = 
= 
(
- объем соленоида). Следовательно, индуктивность соленоида, согласно ее определению (99) равна 
.
Взаимная индукция. Пусть два неподвижных контура расположены близко друг к другу. Если в контуре 1 течет ток 
, он создает через контур 2 полный магнитный поток Ф 2, пропорциональный току
. (101)
Так же, если в контуре 2 течет ток 
, он создает через контур 1 полный магнитный поток Ф 1
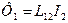. (102)
Коэффициенты 
и 
называют взаимной индуктивностью контуров. Расчет и опыт показывают, что коэффициенты взаимной индуктивности одинаковы при отсутствии ферромагнетиков
= . (103)
Это равенство принято называть теоремой взаимности. Наличие магнитной связи между контурами проявляется в том, что при всяком изменении тока в одном из них в другом возникает эдс индукции. Это явление называют взаимной индукцией. Согласно закону электромагнитной индукции эдс, возникающие в контурах 1 и 2, можно выразить так
Ɛ 1= 
; Ɛ 2= 
. (104)
Трансформатор. Пусть две катушки с числами витков 
и 
намотаны на общий сердечник. Собственно это и есть трансформатор. Он служит для повышения или понижения напряжения. Поскольку магнитное поле в этом случае сосредоточено главным образом в сердечнике, то число линий вектора 
, а также и величина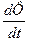 
для обеих катушек будет одинаковым. Считая, что поток пронизывает витков первой катушки и - второй, запишем соответствующие эдс
Ɛ 1= 
; Ɛ 2= 
. (105)
Отношение эдс равно 
. Если считать, что к первой обмотке приложена Ɛ 1 ~ 
, то изменяя число витков во второй катушке, во второй обмотке можно получить повышенное или пониженное напряжение 
.
