Закон Ампера. Каждый носитель тока испытывает действие магнитной силы. Действие этой силы передается проводнику, по которому движутся заряды. В результате магнитное поле действует с определенной силой на сам проводник с током. Величину этой силы и определяет закон Ампера.
Пусть объемная плотность носителей тока в проводнике равна r. В элементе объема dV проводника содержится заряд ρdV, который можно считать точечным вследствие его малости. Тогда элементарная магнитная сила Лоренца, действующая на этот заряд, равна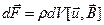 
, где 
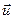- скорость упорядоченного движения зарядов. Плотность тока 
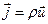, поэтому 
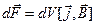. Если ток течет по тонкому проводу, то 
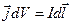, Þ
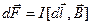. (66)
Это и есть закон Ампера, выражающий силу, действующую на элемент тонкого провода 
, по которому течет ток I.
Теперь можно дать определение основной электрической единицы в системе СИ, ампера [ А ]. Пусть по двум параллельным бесконечно длинным и тонким проводникам течет одинаковый ток I.
По закону Ампера на единицу длины каждого проводника будет действовать сила F = IB 1= IB 2, где магнитные индукции B 1= B 2 определяются формулой (65):
.
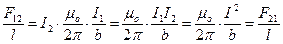Таким образом, сила, действующая на единицу длины любого из проводов, однозначно связана с величиной тока. Силу легко измерить, например, с помощью весов. Отсюда следует определение основной электрической единицы в СИ – единицы силы тока. Ампер [ A ] – это сила постоянного тока, который, проходя по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенных на расстоянии 1 м друг от друга в вакууме, вызывает между ними силу взаимодействия, равную 2∙10-7 Н на каждый метр длины. Единица заряда кулон [Кл] не является основной и определяется через ампер: кулон есть заряд, проходящий за 1 с через поперечное сечение однородного изотропного проводника, по которому течет ток 1 А.
БИЛЕТ №10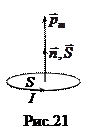 
Магнитный момент контура с током. Рассмотрим плоский контур из тонкого провода достаточно малых размеров, по которому течет ток I. Такой контур называется элементарным. Магнитным моментом элементарного контура называется произведение
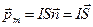, (69)
где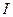 
- ток, 
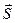- вектор, равный площади контура по величине и совпадающий по направлению с положительной нормалью к контуру (рис.21).
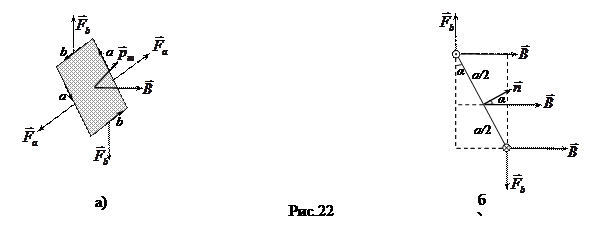
Контур с током в однородном магнитном поле. Если замкнутый контур, по которому течет ток, поместить в однородное магнитное поле, то результирующий момент амперовых сил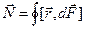 
в общем случае не равен нулю. Действительно, поместим прямоугольную рамку из тонкого провода, по которому течет ток I, в однородное магнитное поле с индукцией 
(рис.22). На рис. 22(а) стороны b расположены перпенди-кулярно вектору , а стороны а – под произвольным углом. На каждую сторону рамки будет действовать своя сила Ампера: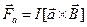 
- на стороны а; 
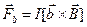- на стороны b, где векторы 
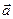и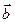 
имеют направление тока на своем участке. Поскольку две силы 
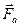лежат в плоскости рамки, равны по модулю и направлены в противоположные стороны, они будут только растягивать (или сжимать) рамку. Пара сил 
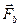не лежит в плоскости рамки, и поэтому создает вращательный момент. Его удобно вычислить, если изобразить рамку по-другому: так, чтобы стороны b были перпендикулярны плоскости листа (рис.22 б). Пара сил 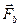создает момент величиной 
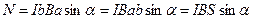, что с учетом (69) можно записать в виде векторного произведения
, (70)
где вектор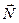 
перпендикулярен как вектору магнитного момента контура 
, так и вектору ; 
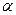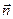- угол между векторами (или 
) и . Если вектор перпендикулярен вектору (плоскость рамки параллельна вектору ), то момент 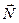максимален, и рамка будет поворачиваться по полю до тех пор, пока эти векторы не станут параллельными. Когда ↑↑ , момент сил 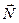=0 и положение контура будет устойчивым. Если ↑↓ , момент сил тоже равен нулю, но положение контура будет неустойчивым.
Покажем, что выбор именно прямоугольного контура, да еще и определенным образом расположенного по отношению к магнитному полю, не нарушает общности полученного выше результата. Действительно, элемент контура произвольной формы можно разложить на две составляющие: параллельную и перпендикулярную вектору . На первую из них сила ампера действовать не будет (sin a =0), а вторая будет вести себя как сторона b прямоугольного контура с током. Поэтому в однородном магнитном поле любой плоский контур с током будет поворачиваться, стремясь установиться своим магнитным моментом параллельно полю.
В неоднородном магнитном поле сила, действующая на контур, уже не будет равна нулю. В частности, сила, действующая на элементарный контур с током, равна (без вывода)
.
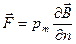Поэтому элементарный контур с током в неоднородном магнитном поле будет не только поворачиваться к положению устойчивого равновесия (при котором ↑↑ ), но и втягиваться в область поля с большей магнитной индукцией .
