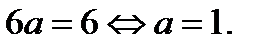Ответ. 
28. Найдите все значения параметра а, при каждом из которых уравнение  имеет единственный корень.
имеет единственный корень.
Решение. Очевидно, для любых значений 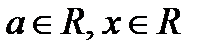 выполняется двойные неравенства
выполняется двойные неравенства 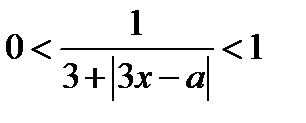 ,
, 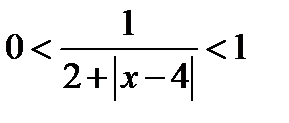 .
.
Обозначим 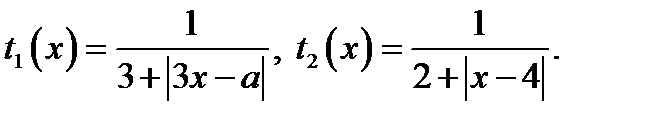 Исходное уравнение принимает вид
Исходное уравнение принимает вид 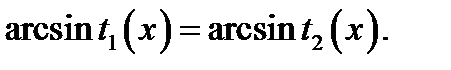
Так как функция  возрастает и
возрастает и 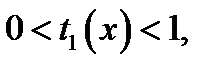
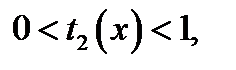 то
то 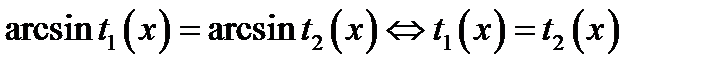 . Тогда последнее уравнение, а значит и исходное уравнение, равносильно уравнению
. Тогда последнее уравнение, а значит и исходное уравнение, равносильно уравнению
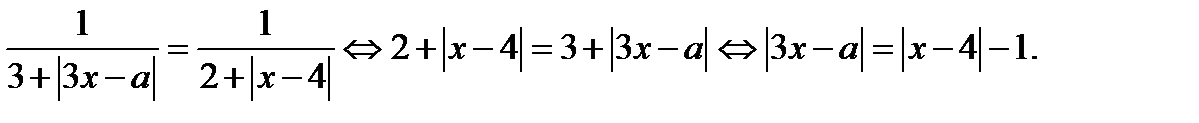
Итак, исходное уравнение равносильно уравнению
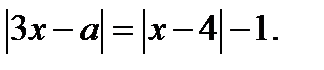 (28.1)
(28.1)
Так как 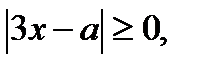 то уравнение (28.1), значит и исходное уравнение, имеет решение, если
то уравнение (28.1), значит и исходное уравнение, имеет решение, если 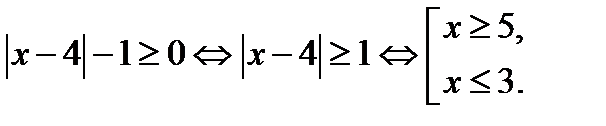
Итак, исходное уравнение имеет решение, если 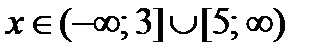 .
.
Найдём, при каких значениях параметра а имеет единственное решение уравнение
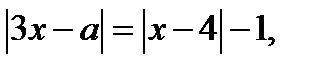 где
где 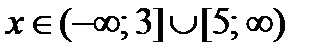 . (28.2)
. (28.2)
Первый способ.
Имеем
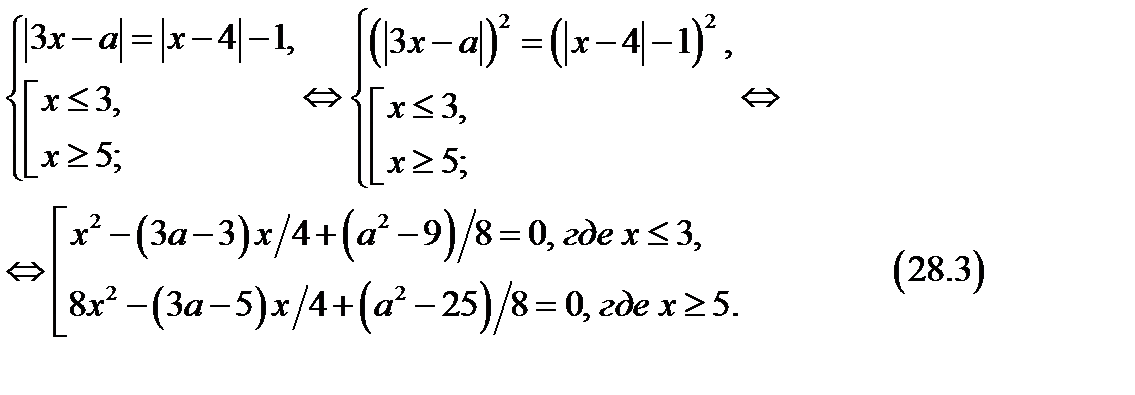
1) Рассмотрим первое уравнение совокупности (28.3).
Это уравнение имеет единственное решение, в двух случаях.
а) Уравнение 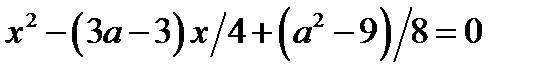 , где
, где 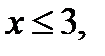 имеет два корня,
имеет два корня,
которые лежат по разные стороны от числа 3. В этом случае рассматриваемое уравнение имеет единственный корень, не равный 3.
Замечание. Квадратное уравнение  имеет два корня, которые лежат по разные стороны от числа
имеет два корня, которые лежат по разные стороны от числа 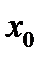 тогда и только, когда
тогда и только, когда 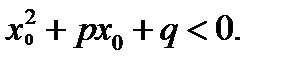
Из замечания следует: уравнение 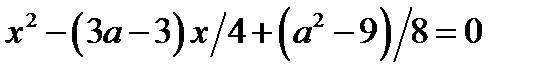 , где
, где 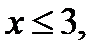 имеет два корня, которые лежат по разные стороны от числа 3 тогда и только, когда
имеет два корня, которые лежат по разные стороны от числа 3 тогда и только, когда
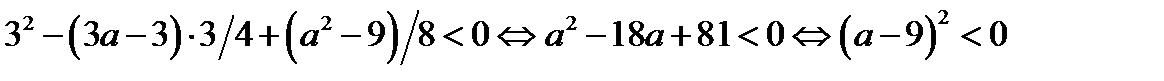
Из последнего неравенства следует: первое уравнение совокупности
(28.3) не имеет корней, которые лежат по разные стороны от числа 3.
б) Корнем уравнения 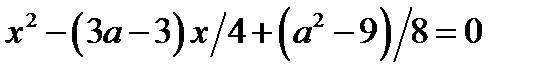 , где
, где 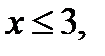 является число 3.
является число 3.
Легко проверить, что число, равное 3, является корнем рассматриваемого уравнения при 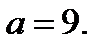
Итак, если 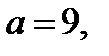 то первое уравнение совокупности (28.3) имеет единственный корень.
то первое уравнение совокупности (28.3) имеет единственный корень.
2) Рассмотрим второе уравнение совокупности (28.3).
Это уравнение имеет единственное решение, в двух случаях.
а) Уравнение 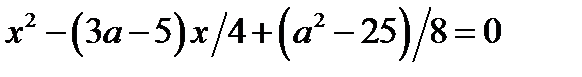 , где
, где 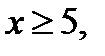 имеет два корня, которые лежат по разные стороны от числа 5. В этом случае рассматриваемое уравнение имеет единственный корень, не равный 5.
имеет два корня, которые лежат по разные стороны от числа 5. В этом случае рассматриваемое уравнение имеет единственный корень, не равный 5.
Из замечания следует: уравнение 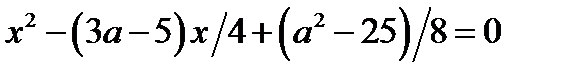 , где
, где 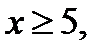 имеет два корня, которые лежат по разные стороны от числа 5 тогда и только, когда
имеет два корня, которые лежат по разные стороны от числа 5 тогда и только, когда
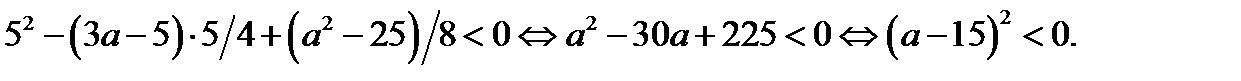
Из последнего неравенства следует: второе уравнение совокупности (28.3) не имеет корней, которые лежат по разные стороны от числа 5.
б) Корнем уравнения 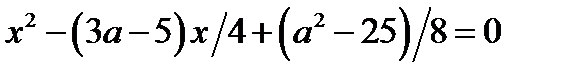 , где
, где 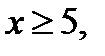 является число 5.
является число 5.
Легко проверить, что число, равное 5, является корнем рассматриваемого уравнения при 
Итак, если 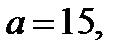 то второе уравнение совокупности (28.2) имеет единственный корень.
то второе уравнение совокупности (28.2) имеет единственный корень.
Так как первое уравнение совокупности (28.3) имеет единствен-
ный корень при 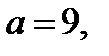 а второе – при
а второе – при 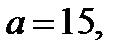 то совокупность (28.3), а значит и исходное уравнение, имеет единственный корень, если
то совокупность (28.3), а значит и исходное уравнение, имеет единственный корень, если 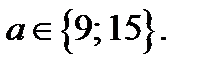
Второй способ.
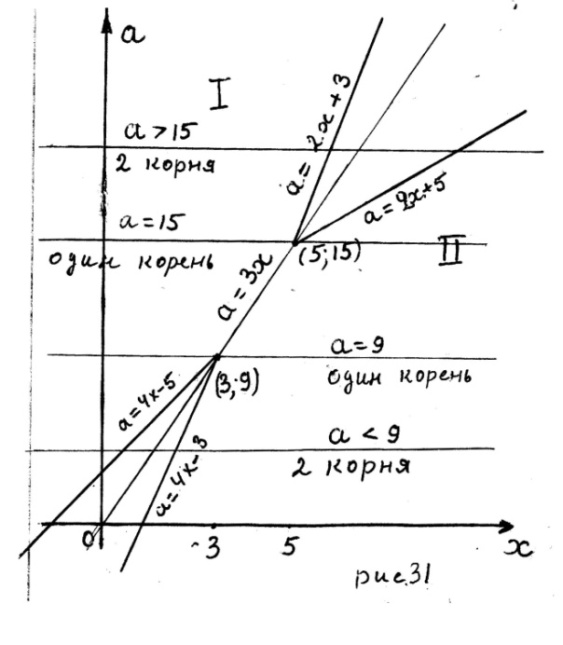
2. На плоскости  построим множество точек, удовлетворяющих уравнению
построим множество точек, удовлетворяющих уравнению 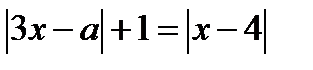 , где
, где 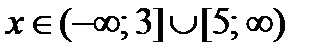 .
.
Для построения множества точек проделаем следующее.
1) Приравняем нулю выражение, стоящие под знаком модуля 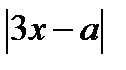 и получим уравнение
и получим уравнение 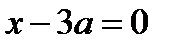 . Построим прямую
. Построим прямую 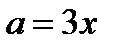 . Эта прямая разобьют плоскость
. Эта прямая разобьют плоскость  на 2 области. В области I выполняется неравенство
на 2 области. В области I выполняется неравенство 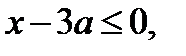 а в области II –
а в области II – 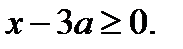
2) Рассмотрим исходное уравнение в каждой области.
В области I, где 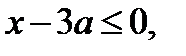 исходное уравнение равносильно уравнению
исходное уравнение равносильно уравнению 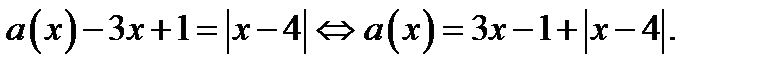
а) Если 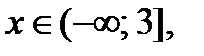 то
то 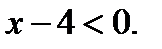 Тогда
Тогда 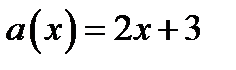 . Прямая
. Прямая 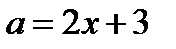 проходит через точки
проходит через точки 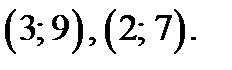 В области I через точки
В области I через точки 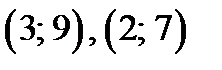 проводим часть прямой
проводим часть прямой 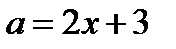 .
.
б) Если 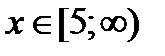 , то
, то 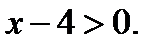 Тогда
Тогда 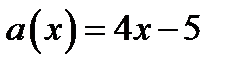 . Прямая
. Прямая 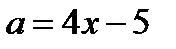
проходит через точки 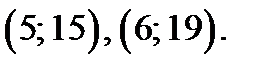 В области I через точки
В области I через точки 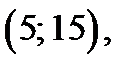
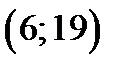 проводим часть прямой
проводим часть прямой 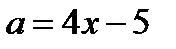 .
.
В области II, где 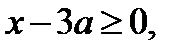 исходное уравнение равносильно уравнению
исходное уравнение равносильно уравнению 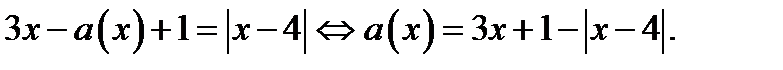
а) Если 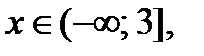 то
то 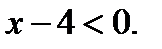
 Тогда
Тогда 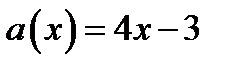 . Прямая
. Прямая 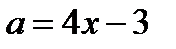 проходит через точки
проходит через точки 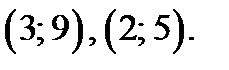 В области II через точки
В области II через точки 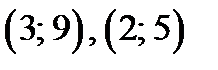 проводим часть прямой
проводим часть прямой 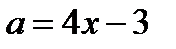 .
.
б) Если 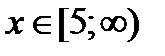 , то
, то 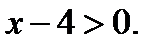 Тогда
Тогда 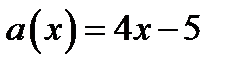 . Прямая
. Прямая 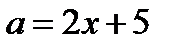 проходит через точки
проходит через точки 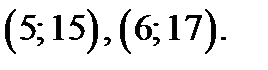 В области II через точки
В области II через точки 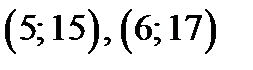 проводим часть прямой
проводим часть прямой 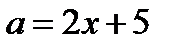 .
.
Из рисунка 31(масштаб на осях координат разный) следует: исходное уравнение, имеет единственный корень, если 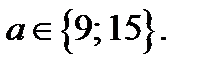
Третий способ.
Рассмотрим функции
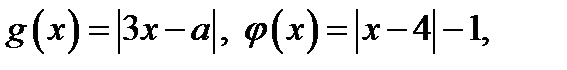 где
где 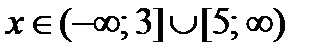 .
.
Графиком функции 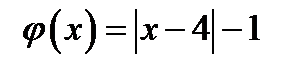 , где
, где 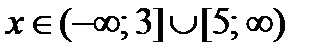 , является «уголок» с вершиной в точке (4;–1), проходящий через точки (3;0) и (5;0).
, является «уголок» с вершиной в точке (4;–1), проходящий через точки (3;0) и (5;0).
Графиком функции 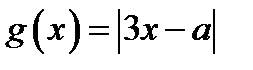 , где
, где 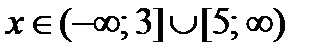 , является «подвижный уголок» с вершиной в точке
, является «подвижный уголок» с вершиной в точке 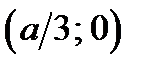 .
.
Рассмотрим следующие случаи.
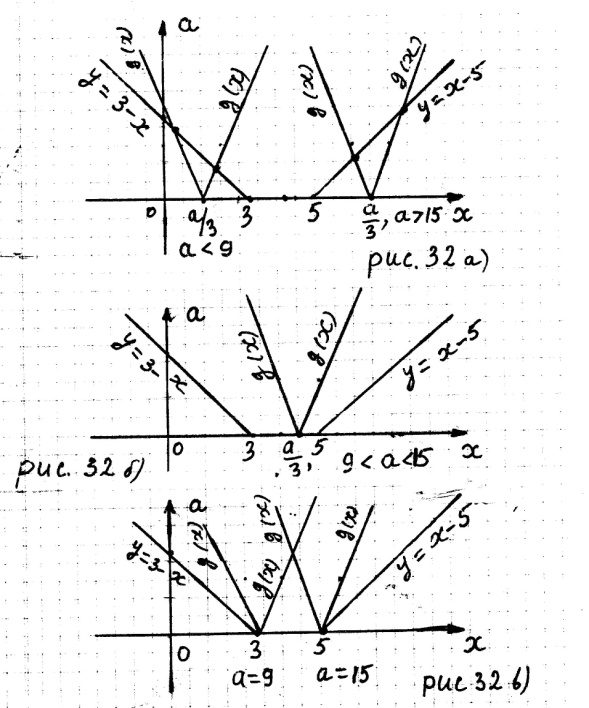 1) Пусть
1) Пусть 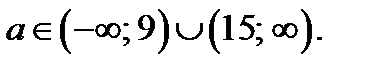
Из рисунка 32 а) следует, что уравнение (28.2), а значит и исходное уравнение, если 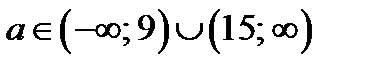 имеет не менее двух корней.
имеет не менее двух корней.
2) Пусть 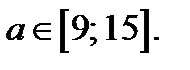
Замечание. Точка пересечения прямых 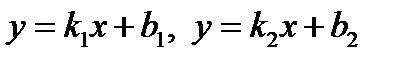 , где
, где 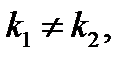 находится из системы
находится из системы 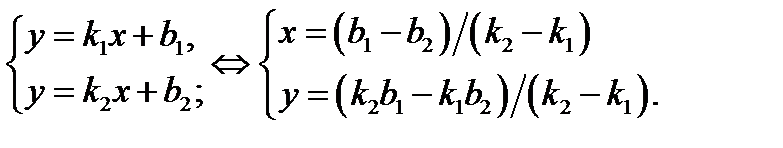
Уравнение (28.2) имеет единственное решение тогда и только тогда, когда имеет решение одна из систем (рис. 32 б), в))
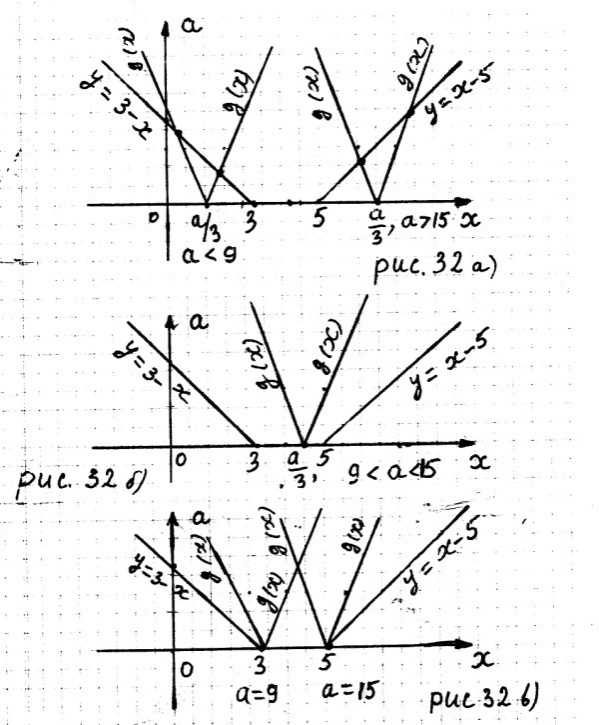
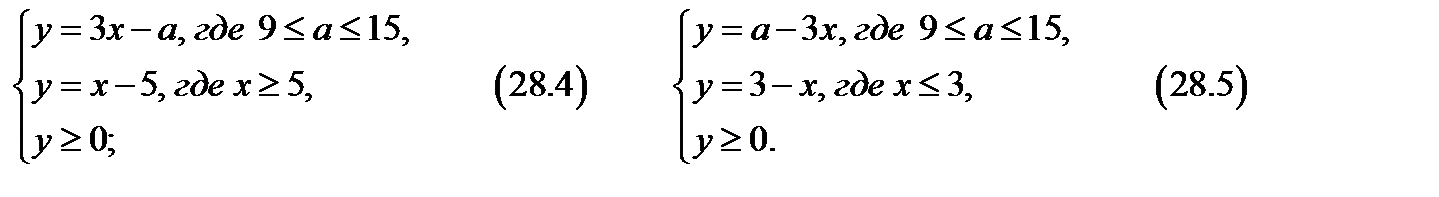 а) Из замечания следует, что ордината точки пересечения системы (28.3) – это
а) Из замечания следует, что ордината точки пересечения системы (28.3) – это 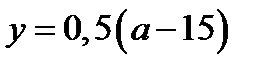 . Система (28.4) имеет решение, если
. Система (28.4) имеет решение, если
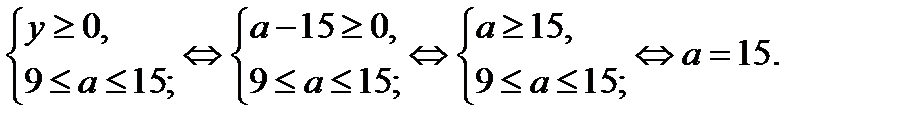
Решением последней системы является 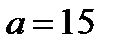 . Решением системы (28.4) является точка (5; 0). Итак, уравнение (28.2), а значит и исходное уравнение при
. Решением системы (28.4) является точка (5; 0). Итак, уравнение (28.2), а значит и исходное уравнение при 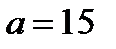 , имеет единственный корень:
, имеет единственный корень: 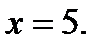
б) Из замечания следует, что ордината точки пересечения системы (28.5) – это 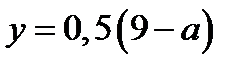 . Система имеет решение, если
. Система имеет решение, если
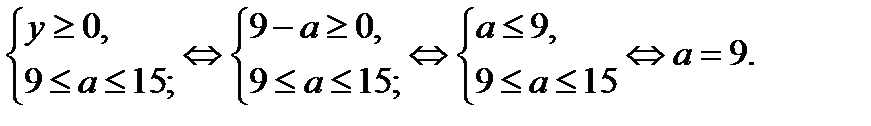
Решением последней системы является 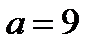 . Решением системы (28.5) является точка (3; 0). Итак, уравнение (28.2), а значит и исходное уравнение при
. Решением системы (28.5) является точка (3; 0). Итак, уравнение (28.2), а значит и исходное уравнение при 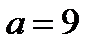 , имеет единственное решение
, имеет единственное решение 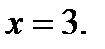
Итак, если 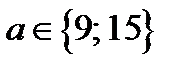 , то уравнение (28.2), а значит и исходное уравнение, имеет единственное решение.
, то уравнение (28.2), а значит и исходное уравнение, имеет единственное решение.
Ответ. 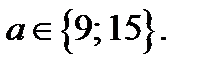
29. Найдите все значения параметра а, если 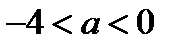 , при которых уравнение
, при которых уравнение 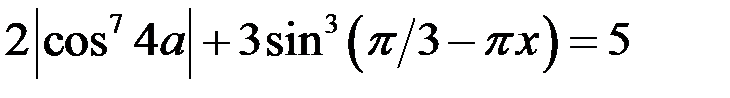 имеет хотя бы одно решение, удовлетворяющее условию
имеет хотя бы одно решение, удовлетворяющее условию 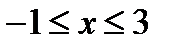 .
.
Решение. 1. Так как 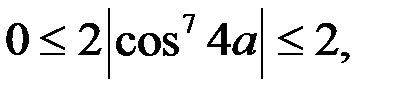
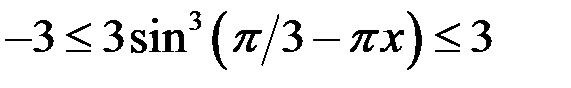 , то левая часть уравнения не больше 5.
, то левая часть уравнения не больше 5.
Так как, левая часть уравнения не больше 5, правая – равна 5, то исходное уравнение равносильно системе
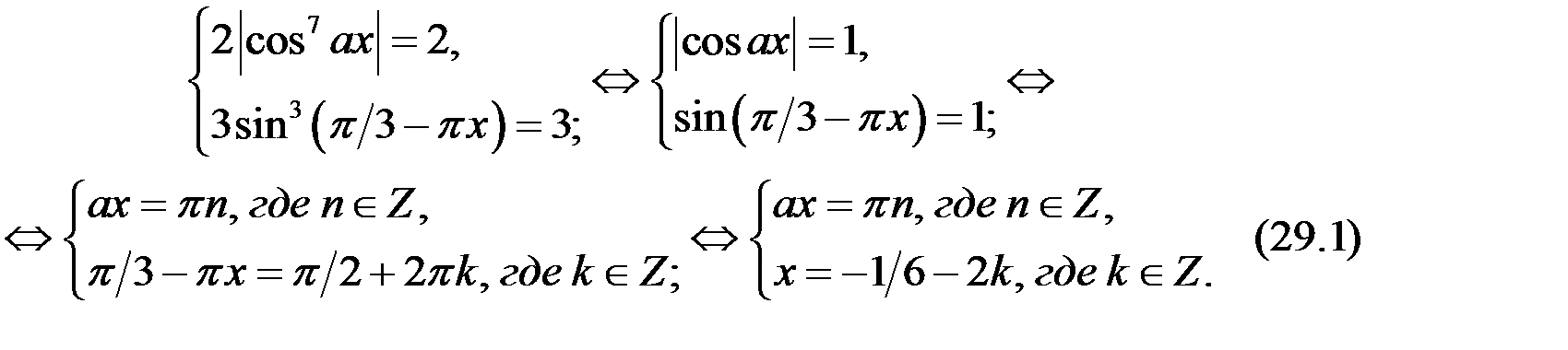
2. Так как по условию задачи 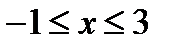 , то из второго уравнения системы (29.1), имеем
, то из второго уравнения системы (29.1), имеем
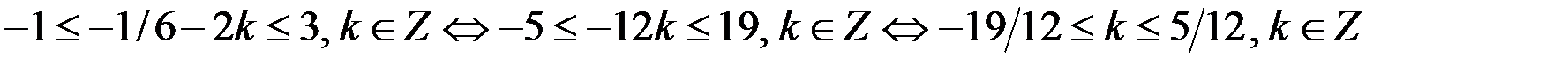 Из последнего двойного неравенства следует, что
Из последнего двойного неравенства следует, что 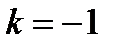 или
или 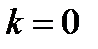 .
.
а) Если 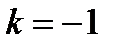 , то
, то 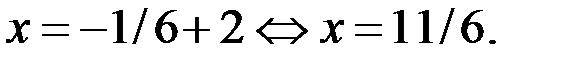
Подставим  в первое уравнение системы (29.1) и получим
в первое уравнение системы (29.1) и получим 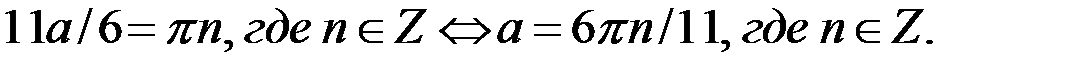
Так как 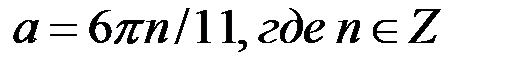 и по условию задачи
и по условию задачи 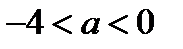 , то
, то
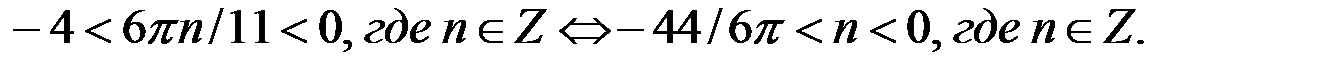
Из последнего двойного неравенства следует, что 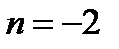 или
или 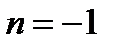 .
.
Если 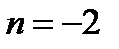 , то
, то 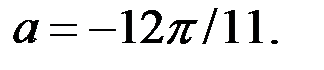 Если
Если 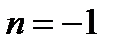 , то
, то 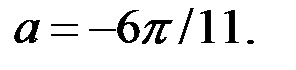
б) Если 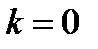 , то
, то 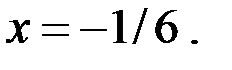
Подставим 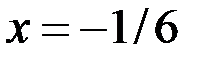 в первое уравнение системы (29.1) и получим
в первое уравнение системы (29.1) и получим
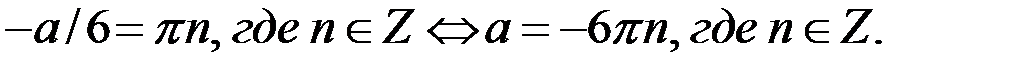
Так как  и по условию задачи
и по условию задачи 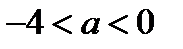 , то
, то
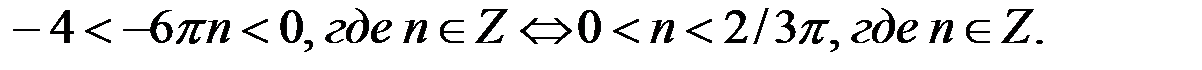
Ни одно значение  не удовлетворяет последнему двойному неравенству.
не удовлетворяет последнему двойному неравенству.
Ответ. 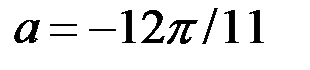 или
или 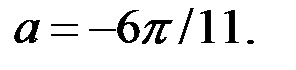
30. Найдите все значения параметра а, при которых уравнение 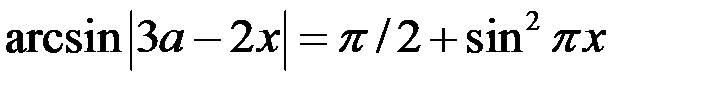 имеет решения. Найдите эти решения.
имеет решения. Найдите эти решения.
Решение. Имеем: 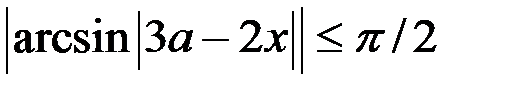 и
и 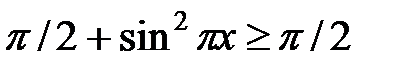 .
.
Таким образом, левая часть данного уравнения не больше 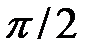 и равна
и равна 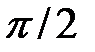 только в случае, когда
только в случае, когда 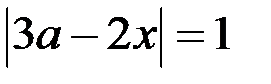 , а правая часть не меньше
, а правая часть не меньше 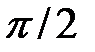 и равна
и равна 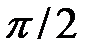 только в случае, когда
только в случае, когда 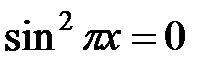 . Тогда исходное уравнение равносильно системе
. Тогда исходное уравнение равносильно системе
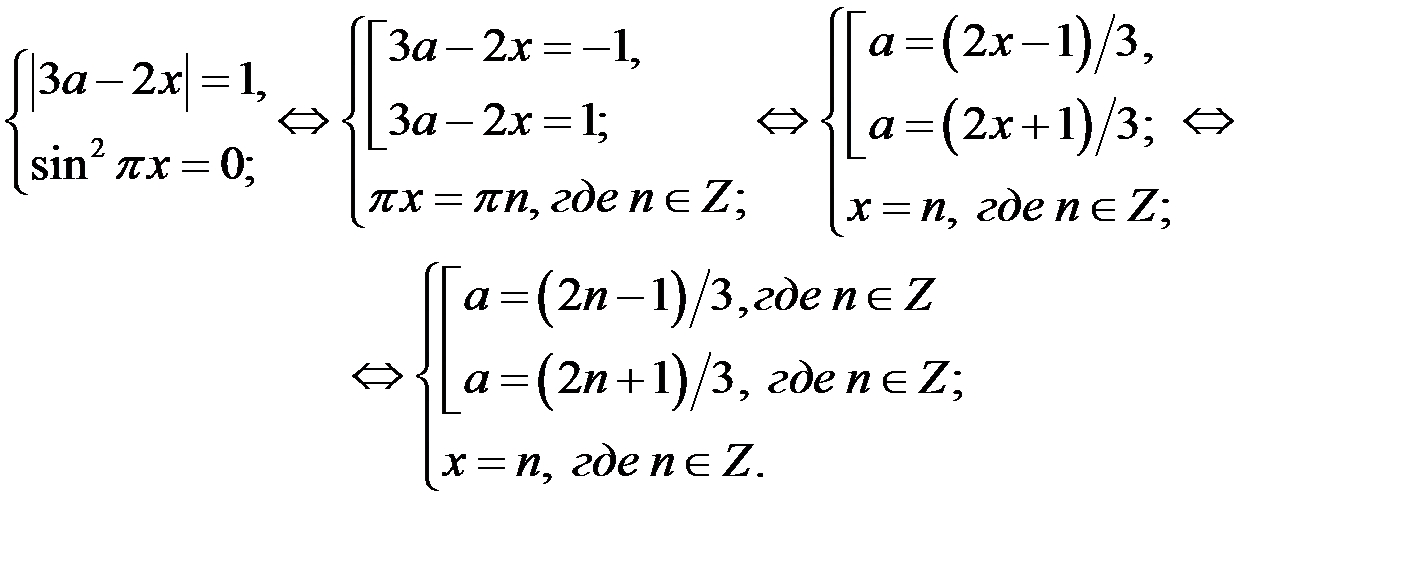
Из последней системы следует ответ.
Ответ. Если 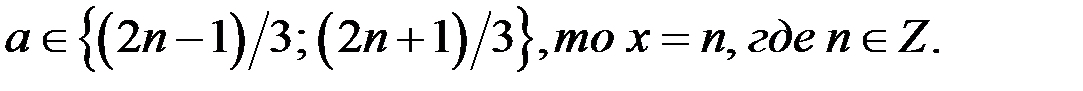
31. Чётная периодическая функция 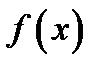 , с периодом
, с периодом 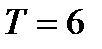 , определённая на всей числовой прямой, на отрезке
, определённая на всей числовой прямой, на отрезке  задана уравнением
задана уравнением 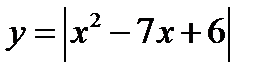 . Найдите все значения параметра а, при которых уравнение
. Найдите все значения параметра а, при которых уравнение 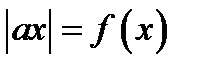 имеет ровно 6 корней.
имеет ровно 6 корней.
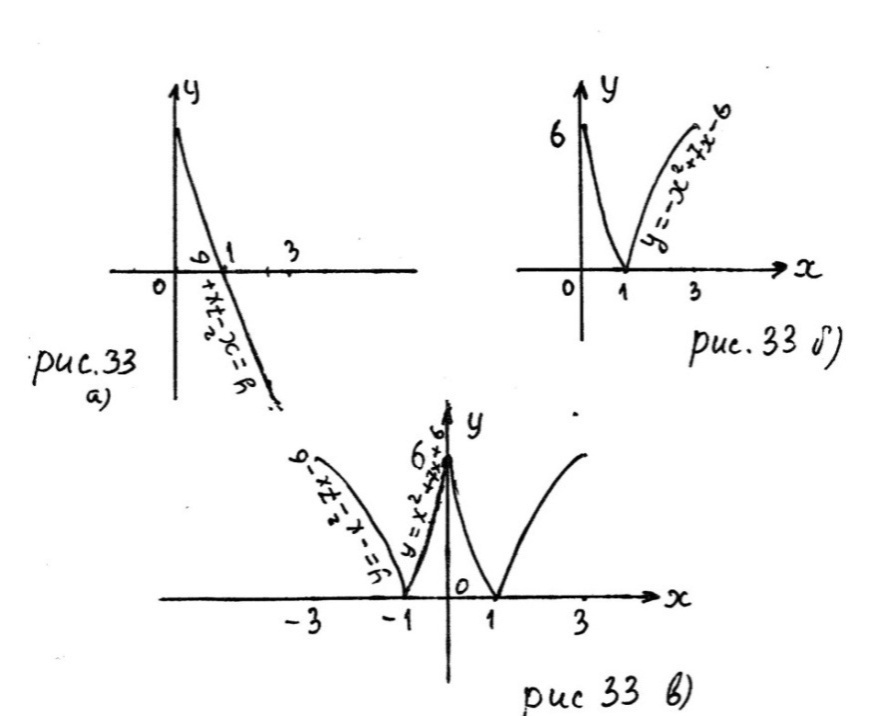
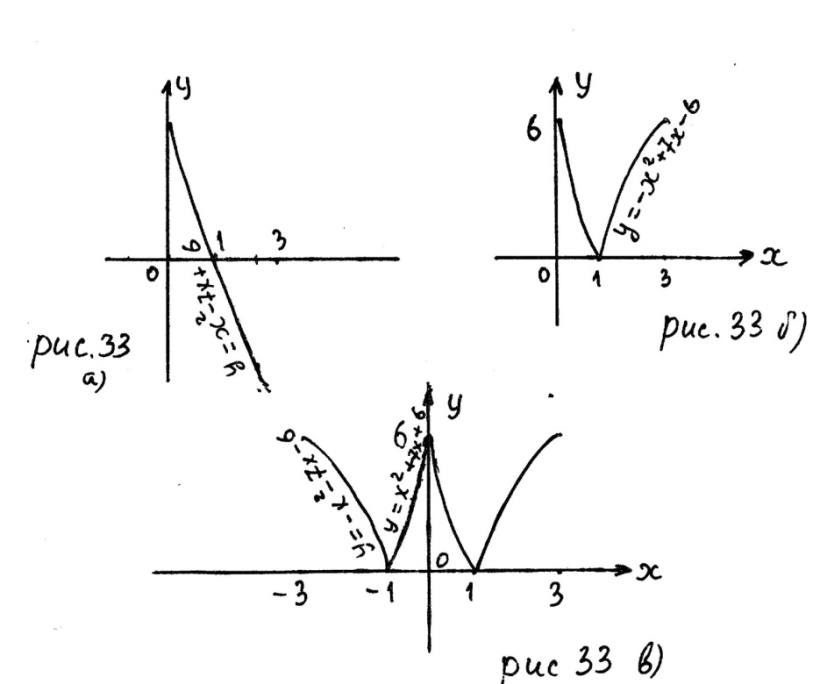
Решение. 1. Построим график функции 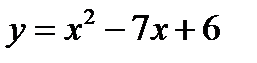 на отрезке
на отрезке  . Имеем
. Имеем 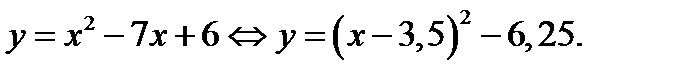
Так как абсцисса вершины параболы 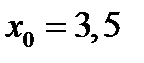 не принадлежит отрезку
не принадлежит отрезку  и ветви параболы направлены вверх, то функция
и ветви параболы направлены вверх, то функция 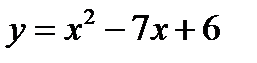 на отрезке
на отрезке  убывает. Поэтому для построения графика части параболы на отрезке
убывает. Поэтому для построения графика части параболы на отрезке  найдём значения:
найдём значения: 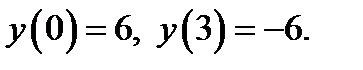
 Точку пересечения параболы
Точку пересечения параболы 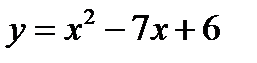 на отрезке
на отрезке  с осью абсцисс находим из системы
с осью абсцисс находим из системы 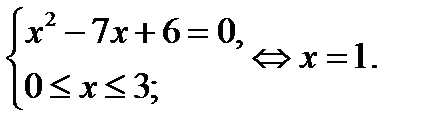
Строим график параболы 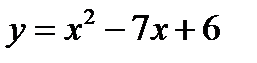 на отрезке
на отрезке  (рис. 33 а)).
(рис. 33 а)).
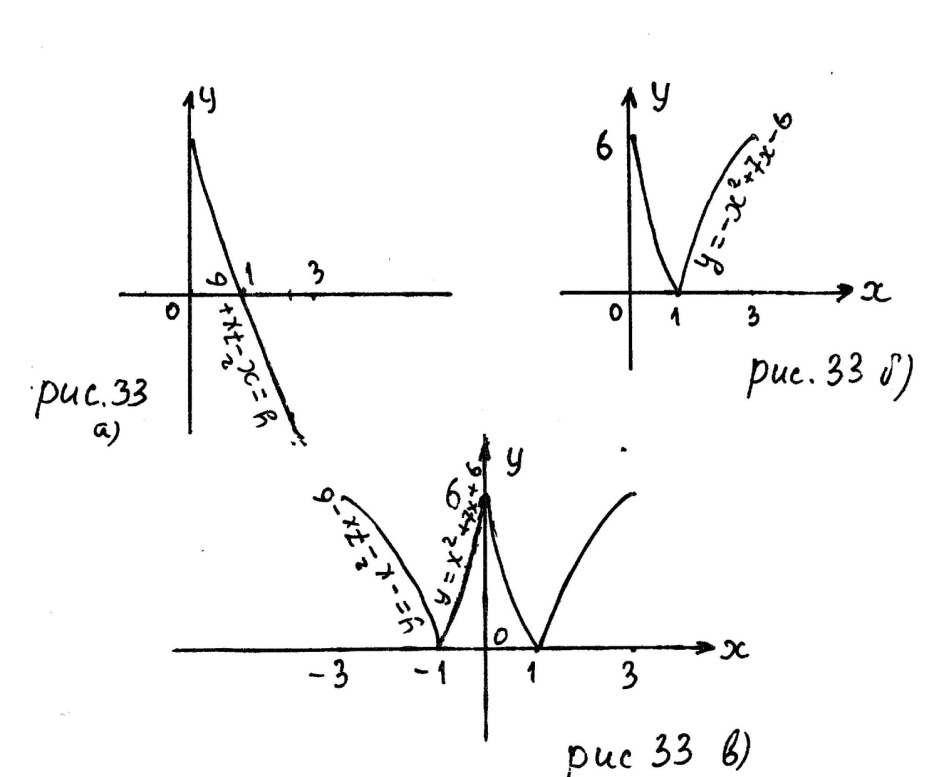
2. Строим график функции 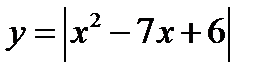 на отрезке
на отрезке  (рис. 33 б)).
(рис. 33 б)).
 3. Построим график функции
3. Построим график функции 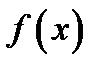 , которая является чётной периодической функцией, с периодом
, которая является чётной периодической функцией, с периодом  , определённая на всей числовой прямой и на отрезке
, определённая на всей числовой прямой и на отрезке  задана уравнением
задана уравнением 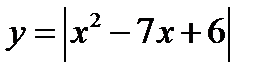 .
.
а) На рисунке 33 в) изображён график функции 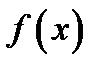 на отрезке
на отрезке 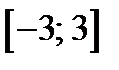 (воспользовались тем, что функции
(воспользовались тем, что функции 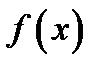 является чётной).
является чётной).
 б) На рисунке 34 изображён график функции
б) На рисунке 34 изображён график функции 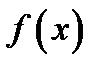 на отрезке
на отрезке 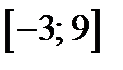 (воспользовались тем, что функции
(воспользовались тем, что функции  является периодической с периодом
является периодической с периодом 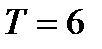 ).
).
Отметим: исходное уравнение имеет бесконечное множество корней, если  и не имеет корней, если
и не имеет корней, если  (рис. 34);
(рис. 34); 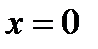 не является корнем исходного уравнения.
не является корнем исходного уравнения.
Замечание. Так как функции 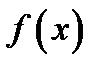 является чётной, то, если пара
является чётной, то, если пара  удовлетворяет уравнению
удовлетворяет уравнению 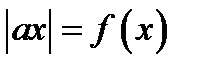 , то и пары
, то и пары 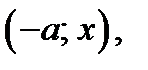
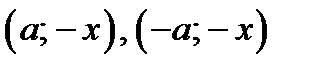 также удовлетворяет этому уравнению.
также удовлетворяет этому уравнению.
Из замечания следует, что исходное уравнение надо рассмотреть при  и
и 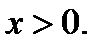 Если при
Если при 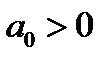 и
и 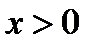 исходное уравнение имеет три корня, то при
исходное уравнение имеет три корня, то при 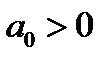 и
и 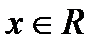 это уравнение имеет шесть корней.
это уравнение имеет шесть корней.
2. Исходное уравнение при  и
и 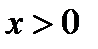 имеет три корня, если графики функций
имеет три корня, если графики функций 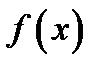 ,
,  пересекаются в трёх точках.
пересекаются в трёх точках.
 а) Из рисунка 34 следует, что графики функций
а) Из рисунка 34 следует, что графики функций 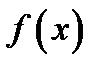 ,
,  при
при 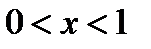 пересекаются в одной точке, если
пересекаются в одной точке, если  .
.
б) Найдём число точек пересечения графиков функций 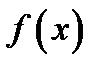 ,
,  , где
, где  , если график функции
, если график функции  проходит через точку А (3; 6). Имеем
проходит через точку А (3; 6). Имеем 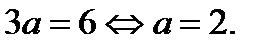
При 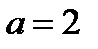 функция
функция  принимает вид
принимает вид 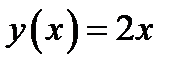 .
.
Число точек пересечения графиков функций 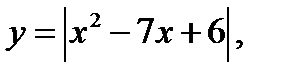
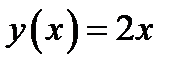 , где
, где 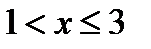 , найдём из системы
, найдём из системы
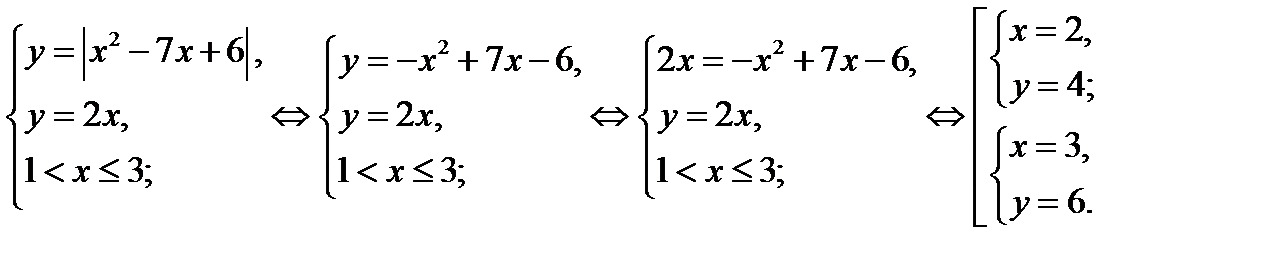
Итак, графики функций 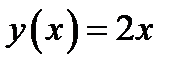 ,
, 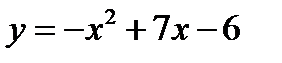 , если
, если 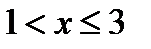 пересекаются в двух точках.
пересекаются в двух точках.
Из а) и б) следует: если 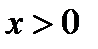 , то графики функций
, то графики функций 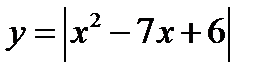 ,
, 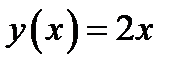 , пересекаются в трёх точках.
, пересекаются в трёх точках.
б) Найдём число точек пересечения графиков функций 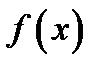 ,
,  , где
, где  , если график функции
, если график функции  проходит через точку А (6; 6). Имеем
проходит через точку А (6; 6). Имеем