Из рисунка 12 в) следует ответ.
Ответ. Один корень, если 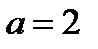 ; два корня, если
; два корня, если  ; нет корней, если
; нет корней, если 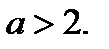
6. Найдите все значения параметра  , при которых уравнение
, при которых уравнение  имеет единственный корень.
имеет единственный корень.
Решение. Рассмотрим функции 
Построим графики функций  и
и  при
при  (областью определения функции
(областью определения функции  является интервал
является интервал  ).
).
Графиком функции  , где
, где  , является «уголок» с вершиной в точке А (2; 1) и сторонами
, является «уголок» с вершиной в точке А (2; 1) и сторонами
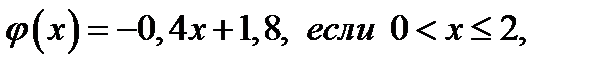

 Функция
Функция  для каждого значения параметра а задаёт семейство логарифмических функций,проходящих точку В (1; 0).
для каждого значения параметра а задаёт семейство логарифмических функций,проходящих точку В (1; 0).
На рисунке 14 а) и изображён график функции  , где
, где  а на рисунке 14 б) изображён график функции
а на рисунке 14 б) изображён график функции  , если
, если  , при некоторых значениях параметра
, при некоторых значениях параметра  .
.
2. Если график функции 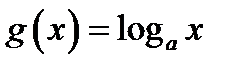 проходит через точку А (2; 1), то он может пересекать график функции
проходит через точку А (2; 1), то он может пересекать график функции  в одной точке А (2; 1) или в двух точках (одна из этих точек А (2; 1)). В этом случае исходное уравнение имеет одно или два корня.
в одной точке А (2; 1) или в двух точках (одна из этих точек А (2; 1)). В этом случае исходное уравнение имеет одно или два корня.
График функции  проходит через точку А (2; 1), если
проходит через точку А (2; 1), если

При 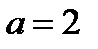 исходное уравнение принимает вид
исходное уравнение принимает вид
 (6.1)
(6.1)
3. Уравнение (6.1) равносильно совокупности уравнений
 (6.2)
(6.2)
1) Рассмотрим первое уравнение совокупности (6.2).
Так как функция 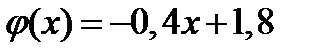 убывает, а функция
убывает, а функция 
возрастает, то графики этих функций пересекаются только в одной точке – это точка А (2; 1), а тогда уравнение (6.1) при  , а значит и исходное уравнение при
, а значит и исходное уравнение при 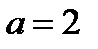 и
и  , имеет единственный корень:
, имеет единственный корень:  .
.
2) Рассмотрим второе уравнение совокупности (6.2).
Найдём число точек пересечений графиков функций  ,
,
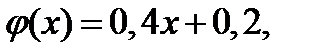 при
при 
Рассмотрим функцию

Найдём промежутки монотонности, точки экстремума функции 
а) Найдём производную функции  . Имеем
. Имеем

б) Из уравнения  находим критические точки. Имеем
находим критические точки. Имеем 
(Отметим: 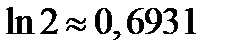 ).
).
б) Критическая точка  разбивает интервал
разбивает интервал  на интервалы
на интервалы  , на каждом из которых
, на каждом из которых  сохраняет знак.
сохраняет знак.
 в) Определим знаки функции
в) Определим знаки функции  . Знаки функции
. Знаки функции  показаны на рисунке 13.
показаны на рисунке 13.
г) Из рисунка 13. делаем вывод.
Функция  убывает на промежутке
убывает на промежутке  и возрастает на промежутке
и возрастает на промежутке  (критическая точка, в которой функция
(критическая точка, в которой функция  определена, принадлежит и промежутку возрастания, и промежутку убывания).
определена, принадлежит и промежутку возрастания, и промежутку убывания).
В точке  функция
функция  имеет минимум. Так как функция
имеет минимум. Так как функция  убывает на промежутке
убывает на промежутке  и
и  то на этом промежутке функция
то на этом промежутке функция  отрицательная. Тогда
отрицательная. Тогда  .
.
Замечание. Если функция  непрерывна на отрезке [ a; b ] и на концах отрезка имеет значения разных знаков, то существует такая точка
непрерывна на отрезке [ a; b ] и на концах отрезка имеет значения разных знаков, то существует такая точка  что
что 
Вычислим: 
Так как  ,
,  и функция
и функция  непрерывна при
непрерывна при  , то существует такая точка
, то существует такая точка  что
что  Это означает, что функции
Это означает, что функции  и
и  пересекаются в точке
пересекаются в точке  Тогда уравнение (6.1) при
Тогда уравнение (6.1) при 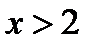 , а значит и исходное уравнение при
, а значит и исходное уравнение при 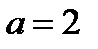 и
и 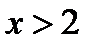 , имеет корень.
, имеет корень.
Из 1) и 2) следует, что исходное уравнение при 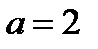 имеет два корня.
имеет два корня.
4. Построим графики функций  и
и  , если
, если  при
при  .
.
Для этого воспользуемся следующим: так как  то найдётся такое значение
то найдётся такое значение 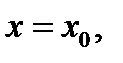 что для всех
что для всех 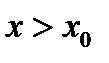 выполняется неравенство
выполняется неравенство 
На рисунке 14 в) изображены графики функций  где
где  , и
, и  если
если  и
и  . Из рисунка 14 в) следует, что уравнение
. Из рисунка 14 в) следует, что уравнение  ни при каких значениях параметра
ни при каких значениях параметра  не имеет единственного корня.
не имеет единственного корня.
Ответ. 
7. При каких значениях параметра а уравнение  имеет единственный корень; имеет два корня; не имеет корней?
имеет единственный корень; имеет два корня; не имеет корней?
Решение. Так как  то исходное уравнение имеет решение, если
то исходное уравнение имеет решение, если

Рассмотрим функции  ,
,  , где
, где 
1. На плоскости  построим график функции
построим график функции  , где
, где  Имеем
Имеем

Найдём: 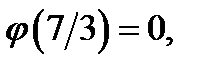

 и построим график функции
и построим график функции  , где
, где 
Для каждого значения параметра  функция
функция  задаёт семействопоказательных функций, которые проходят
задаёт семействопоказательных функций, которые проходят
через точку В (0; 1).
На рисунках 15 а) и б) соответственно изображены графики функций  и
и  , где
, где 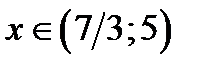 .
.
 2. Если график функции
2. Если график функции  проходит через точку А (3; 2), то он может пересекать график функции
проходит через точку А (3; 2), то он может пересекать график функции  в одной точке А (3; 2) или в двух точках (одна из этих точек А (3; 2)). В этом случае исходное уравнение имеет одно или два корня.
в одной точке А (3; 2) или в двух точках (одна из этих точек А (3; 2)). В этом случае исходное уравнение имеет одно или два корня.
График функции  проходит через точку А (3; 2), если
проходит через точку А (3; 2), если
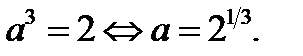
При 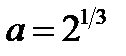 исходное уравнение принимает вид
исходное уравнение принимает вид
 , где
, где  (7.1)
(7.1)
3. Уравнение (7.1) равносильно совокупности уравнений
 (7.2)
(7.2)
1) Рассмотрим первое уравнение совокупности (7.2).
Найдём число точек пересечений графиков функций  и
и  , где
, где 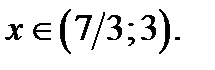
Рассмотрим функцию

Найдём промежутки монотонности функции 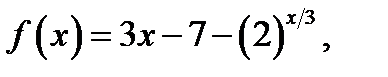

а) Найдём производную функции  . Имеем
. Имеем

б) Определим знак 
Так как  , то
, то  . Так как функция
. Так как функция 
возрастает, то  , а тогда
, а тогда


Таким образом,  если
если  Тогда функция
Тогда функция  возрастает на интервале
возрастает на интервале 
в) Так как  и функция
и функция  возрастает на интервале
возрастает на интервале  , то имеем
, то имеем

Из последней системы следует, что графики функций  и
и  не пересекаются при
не пересекаются при 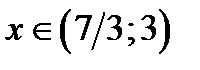 . Это означает, что уравнение (7.1) при
. Это означает, что уравнение (7.1) при 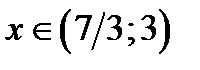 , а значит и исходное уравнение при
, а значит и исходное уравнение при  и
и 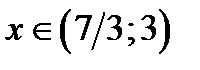 , не имеет корней.
, не имеет корней.
2) Рассмотрим второе уравнение совокупности (7.2).
Так как функция  убывает, а функция
убывает, а функция  возрастает, то графики этих функций пересекаются только в одной точке – это точка А (3; 2), а тогда уравнение (7.1) при
возрастает, то графики этих функций пересекаются только в одной точке – это точка А (3; 2), а тогда уравнение (7.1) при 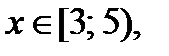 а значит и исходное уравнение при
а значит и исходное уравнение при  и
и 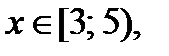 имеет единственный корень.
имеет единственный корень.
Из 1) и 2) следует, что уравнение (7.1), а значит и исходное при  , имеет единственный корень.
, имеет единственный корень.
На рисунке 15 в) изображены графики функций  , где
, где  ,
,  , где
, где 
Из рисунка следует ответ.
Ответ. Если  то корней нет; если
то корней нет; если  то единственный корень; если
то единственный корень; если 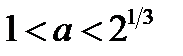 или
или  , то два корня.
, то два корня.
8. Найдите все значения параметра а, при которых уравнение  не имеет решений.
не имеет решений.
Решение 1. Имеем

Исходное уравнение не имеет решений, если одновременно не имеют решений оба уравнения совокупности (8.1).
Возможны следующие случаи.
1) Если 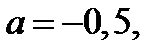 то первое уравнения совокупности (8.1) не имеет
то первое уравнения совокупности (8.1) не имеет
решений, а второе уравнение – имеет решение (это легко проверить). Это означает, что исходное уравнение при  имеет решение.
имеет решение.
2) Если  то второе уравнения совокупности (8.1) не имеет решений. Первое уравнение совокупности (8.1) при
то второе уравнения совокупности (8.1) не имеет решений. Первое уравнение совокупности (8.1) при  принимает вид
принимает вид 
Так как уравнение 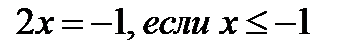 не имеет решений, то и первое уравнения совокупности (8.1) не имеет решений Это означает, что исходное уравнение при
не имеет решений, то и первое уравнения совокупности (8.1) не имеет решений Это означает, что исходное уравнение при  не имеет решений.
не имеет решений.
3) Если 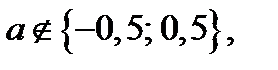 то исходное уравнение равносильно совокупности
то исходное уравнение равносильно совокупности

Совокупность (8.2) не имеет решений при тех значениях параметра а, которые удовлетворяют системе

Из последнего двойного неравенства следует, что исходное уравнение при  не имеет решений.
не имеет решений.
Из 2) и 3) следует ответ.
Ответ.  .
.
9. Найдите все значения параметра а, при которых уравнение
 имеет не менее двух решений.
имеет не менее двух решений.
Решение. 1. На плоскости  построим множество точек, удовлетворяющих уравнению
построим множество точек, удовлетворяющих уравнению 
 .
.
Найдём нули выражений, стоящих под знаком модуля:

Нули выражений, стоящих под знаком модуля: 


2. Так как функция  линейная на каждом промежутке
линейная на каждом промежутке  ,
,  ,
,  ,
,  , то для построения графика функции
, то для построения графика функции  проделаем следующее.
проделаем следующее.
1) Найдём значения функции  в точках
в точках 

 и в
и в
точках  (принадлежит промежутку
(принадлежит промежутку  ) и
) и  (принадлежит интервалу
(принадлежит интервалу  ). Имеем
). Имеем 
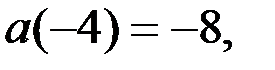


 .
.
2) На плоскости  построим точки: (–5; –9), (–4; –8), (0;4), (4;0), (5;1).
построим точки: (–5; –9), (–4; –8), (0;4), (4;0), (5;1).
 3) На каждом промежутке
3) На каждом промежутке  ,
,  ,
,  ,
,  построим часть прямой, проходящей через точки абсциссы, которых принадлежат соответствующему промежутку.
построим часть прямой, проходящей через точки абсциссы, которых принадлежат соответствующему промежутку.
Исходное уравнение будет иметь не менее двух решений при тех значениях параметра  , при которых прямые
, при которых прямые  пересекают график функции
пересекают график функции 

 в двух или трех точках (рис 16). Из рисунка 16 следует ответ.
в двух или трех точках (рис 16). Из рисунка 16 следует ответ.
Ответ.  .
.
10. Найдите все значения параметра а, при которых уравнение  имеет хотя бы один корень.
имеет хотя бы один корень.
Решение. 1. Перепишем уравнение в виде 
Так как 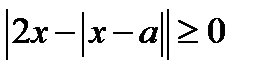 , то последнее уравнение, а значит и исходное уравнение может иметь решение, если
, то последнее уравнение, а значит и исходное уравнение может иметь решение, если

Рассмотрим исходное уравнение при  .
.
2. Запишем уравнение в виде 
Рассмотрим функцию  где
где  .
.
а) Если  , то при любом раскрытии модулей имеем
, то при любом раскрытии модулей имеем

Очевидно,  Тогда функция
Тогда функция  (линейная) при
(линейная) при  возрастает.
возрастает.
б) Если  , то при любом раскрытии модулей имеем
, то при любом раскрытии модулей имеем
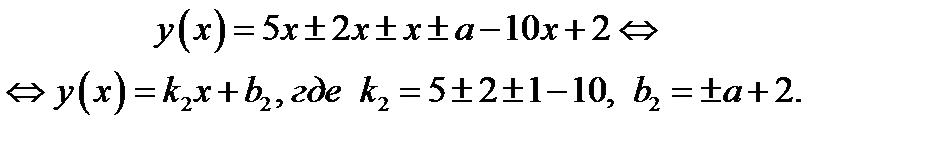
 Очевидно,
Очевидно,  Тогда функция
Тогда функция  при
при  убывает.
убывает.
Так как при  функция
функция  возрастает, а при
возрастает, а при  – убывает, то точка
– убывает, то точка  – точка максимума.
– точка максимума.
Определим знаки функции  в точках
в точках  и
и 






