1. Сколько корней в зависимости от параметра а имеетуравнение 
? Найдите эти корни.
Решение. 1. Приравняем нулю выражения, стоящие под знаком модуля: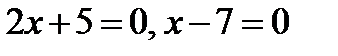 
. Точки 
и 
разбивают числовую ось на три промежутка: 
.
2. Рассмотрим исходное уравнение на каждом промежутке.
Замечание. При раскрытии модуля надо учитывать знак выражения, стоящего под модулем на соответствующем промежутке. Так как знак выражения на каждом промежутке постоянный, то знак выражения на промежутке совпадает со знаком выражения в любой точке этого промежутка.
Раскрывая модули, заменим исходное уравнение равносильной совокупностью трёх уравнений:
а) Рассмотрим первое уравнение совокупности (1.1).
Корнем исходного уравнения на промежутке 
является 
, если
Итак, корнемисходного уравнения на промежутке является 
, если 
б) Рассмотрим второе уравнение совокупности (1.1).
Корнем исходного уравнения на промежутке 
является 
, если
Итак, корнем исходного уравнения на промежутке является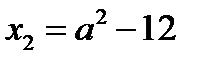 
, если 
в) Рассмотрим третье уравнение совокупности (1.1).
Корнем исходного уравнения на промежутке 
является
, если 
Итак, корнем исходного уравнения на промежутке является 
, если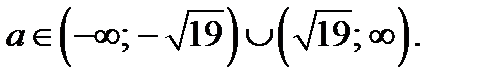 
Нанесём корни уравнения на числовую прямую параметра (рис.7).
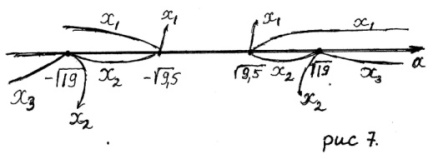Ответ. Если 
, то нет корней; если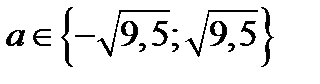 
, то один корень 
; если 
, то два корня , ; если 
, то два корня , 
.
Графический метод
2. Найдите все значения параметра а, при которых уравнение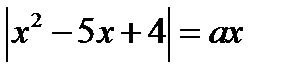 
имеет не менее трёх корней.
Решение. Рассмотрим функции 
Уравнение 
задаёт семейство прямых, проходящих через начало координат (исключая ось ординат). На рисунке 8 изображён график функции 
а также графики представителей семейства .
Отметим. Парабола и прямая (не параллельная оси ординат) могут 1) пересекаться в одной точке (прямая является касательной к параболе); 2) пересекаться в двух точках; 3) не пересекаться.
Исходное уравнение имеет три корня при тех значениях параметра а, при которых графики функций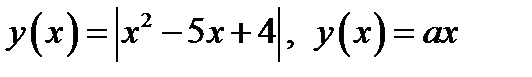 
пересекаются в трёх точках.
Если касательной к параболе 
является прямая 
и абсцисса точки касания 
, то прямая
пересекает график функции 
в трёх точках (рис. 8).
Найдём значение параметра 
.
Отметим: прямая 
является касательной к параболе 
, если имеет единственное решение система уравнений
Последняя система имеет единственное решение, если имеет единственное решение квадратное уравнение 
Прямая является касательной к параболе , если имеет единственное решение квадратное уравнение
.
Квадратное уравнение 
имеет единственное решение при тех значениях параметра 
, при которых равен нулю дискриминант D этого уравнения. Имеем
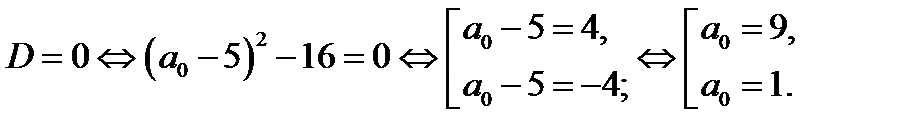Так как дискриминант D квадратного уравнения равен нулю при 
или 
то решением квадратного уравнения является 
, где или 
Точка является абсциссой точки касания прямой и параболы. Если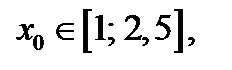 
то прямая пересекает график функции в трёх точках.
Если , то 
не удовлетворяет условию 
.
Если то 
, удовлетворяет условию 
. Тогда
прямая 
пересекает график функции в трёх точках. Итак, исходное уравнение при 
имеет три корня.
2. Исходное уравнение имеет четыре корня при тех значениях параметра а, при которых графики функций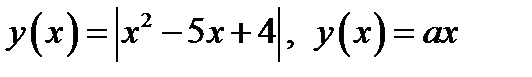
пересекаются в четырёх точках.
Из рисунка 8 следует, что прямая 
, где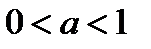 
, пересекает график функции 
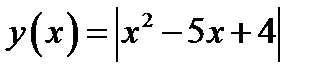в четырёх точках. Тогда исходное уравнение при 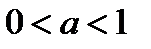имеет четыре корня.
Ответ. 
.
