3. Решите уравнение  .
.
Решение. На плоскости  построим множество точек, удовлетворяющих исходному уравнению.
построим множество точек, удовлетворяющих исходному уравнению.
Для построения множества точек проделаем следующее.
1. Приравняем нулю выражения, стоящие под знаком модуля:  и
и 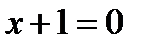 . Откуда следует:
. Откуда следует:  и
и  .
.
На плоскости  построим прямые
построим прямые  и
и  . Эти прямые разобьют плоскость
. Эти прямые разобьют плоскость  на 4 области.
на 4 области.
2. Рассмотрим исходное уравнение в каждой области. Для этого надо раскрыть модули в каждой области.
Замечание. При раскрытии модулей надо учитывать знак выражения, стоящего под модулем в соответствующей области. Так как знак в каждой области постоянный, то знак выражения в области совпадает со знаком выражения в любой точке этой области.
1) В области I исходное уравнение равносильно системе


В области I строим часть прямой  , которая параллельна прямой
, которая параллельна прямой  и пересекает прямую
и пересекает прямую 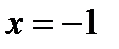 в точке А (–1; 3,5).
в точке А (–1; 3,5).
2) В области II исходное уравнение равносильно системе

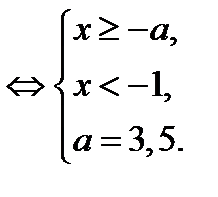
В области II строим часть прямой  , которая параллельна оси абсцисс и пересекает прямые
, которая параллельна оси абсцисс и пересекает прямые 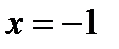 и
и  соответственно в точках А (–1; 3,5) и В (–3,5; 3,5).
соответственно в точках А (–1; 3,5) и В (–3,5; 3,5).
3) В области III исходное уравнение равносильно системе
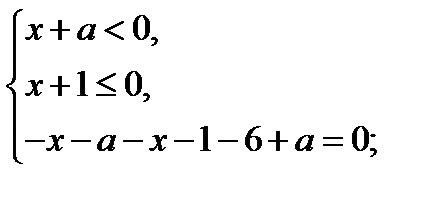

 В области III строим часть прямой
В области III строим часть прямой  , которая параллельна оси ординат и пересекает прямую
, которая параллельна оси ординат и пересекает прямую  в точке В (–3,5; 3,5).
в точке В (–3,5; 3,5).
4) В области IV исходное уравнение равносильно системе


Ни одна точка не удовлетворяет последней системе.
График исходного уравнения изображён на рисунке 9 (графиком исходного уравнения является совокупность части прямых:  ,
,  ,
,  ). Для того чтобы найти решения исходного уравнения при каждом значении параметра
). Для того чтобы найти решения исходного уравнения при каждом значении параметра  , надо провести прямые
, надо провести прямые  (если прямая
(если прямая  пересекает график исходного уравнения в n точках,тоисходное уравнение при
пересекает график исходного уравнения в n точках,тоисходное уравнение при  имеет n решений) и найти абсциссы точек пересечения графиков исходного уравнения и прямой
имеет n решений) и найти абсциссы точек пересечения графиков исходного уравнения и прямой  . Из рисунка 9 следует ответ.
. Из рисунка 9 следует ответ.
Ответ. При  уравнение не имеет решений; при
уравнение не имеет решений; при 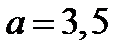 решением уравнении являются
решением уравнении являются  (уравнение имеет бесконечное множество решений); при
(уравнение имеет бесконечное множество решений); при  уравнение имеет два решения
уравнение имеет два решения  ,
, 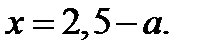
4. Сколько решений в зависимости от параметра а имеетуравнение  на отрезке
на отрезке  ?
?
Метод интервалов.
Решение. 1. Если 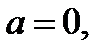 то уравнение на отрезке
то уравнение на отрезке  не имеет решений, так как оно принимает вид
не имеет решений, так как оно принимает вид 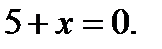
2. Пусть 
Имеем 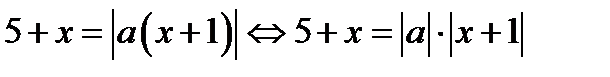 .
.
Замечание. Если пара  удовлетворяет уравнению, то и пара
удовлетворяет уравнению, то и пара  также удовлетворяет этому уравнению.
также удовлетворяет этому уравнению.
Из замечания и 1. следует: уравнение надо рассмотреть при 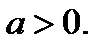
Если  , то исходное уравнение равносильно уравнению
, то исходное уравнение равносильно уравнению
 , где
, где  и
и  (4.1)
(4.1)
Раскрывая модули, на отрезке  заменим уравнение (4.1) равносильной совокупностью уравнений
заменим уравнение (4.1) равносильной совокупностью уравнений
 2) Рассмотрим первое уравнение совокупности (4.2), если
2) Рассмотрим первое уравнение совокупности (4.2), если 
Так как  то
то 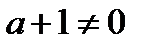 , а тогда
, а тогда 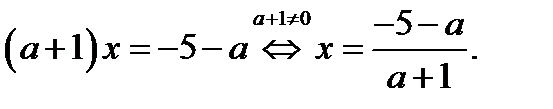
Решением уравнения (4.1), а значит и исходного уравнения, на отрезке  является
является  , если
, если

Итак, если  , то
, то 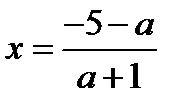 является решением уравнения (4.1), а значит и исходного уравнения на отрезке
является решением уравнения (4.1), а значит и исходного уравнения на отрезке  .
.
3) Рассмотрим второе уравнение совокупности (4.2), если 
а) Если 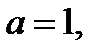 то легко проверить, что уравнение
то легко проверить, что уравнение  , а значит и исходное уравнение, не имеет решений.
, а значит и исходное уравнение, не имеет решений.
б) Пусть  Тогда
Тогда

Решением уравнения (4.1), а значит и исходного уравнения, на
промежутке  при
при  является
является  , если
, если

Итак, если 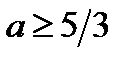 , то
, то  является решением уравнения (4.1), а значит и исходного уравнения на промежутке
является решением уравнения (4.1), а значит и исходного уравнения на промежутке  .
.
Из 1. и 2. с учётом замечания следует ответ.
Ответ. Если  , то нет решений; если
, то нет решений; если  , то одно решение; если
, то одно решение; если  , то два решения.
, то два решения.
Метод областей.
Решение. На плоскости  построим множество точек, удовлетворяющих уравнению
построим множество точек, удовлетворяющих уравнению
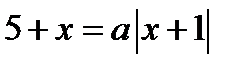 , где
, где  и
и  (4.3).
(4.3).
Уравнение (4.3) равносильно совокупности (см. первый метод)
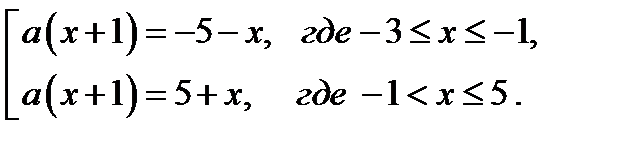 (4.2)
(4.2)
Легко проверить, что  не удовлетворяет исходному уравнению. Поэтому рассмотрим первое уравнение совокупности (4.2) при
не удовлетворяет исходному уравнению. Поэтому рассмотрим первое уравнение совокупности (4.2) при  . Имеем
. Имеем

 На отрезке
На отрезке  строим часть гиперболы
строим часть гиперболы  , асимптотой которой является прямая
, асимптотой которой является прямая  . Гипербола пересекает прямую
. Гипербола пересекает прямую  в точке А
в точке А  .2. Второе уравнение совокупности (4.2) равносильно системе
.2. Второе уравнение совокупности (4.2) равносильно системе

На промежутке  строим часть гиперболы
строим часть гиперболы 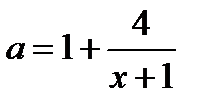 , асимптотой которой является прямая
, асимптотой которой является прямая  . Гипербола пересекает пря-
. Гипербола пересекает пря-
мую  в точке В
в точке В  .
.
График уравнения (4.3) изображён на рисунке 10.
Из рисунка 10 для  и замечания следует ответ.
и замечания следует ответ.
Ответ. Если  , то нет решений; если
, то нет решений; если  , то одно решение; если
, то одно решение; если  , то два решения.
, то два решения.
Графический метод.
Решение. Если  , то исходное уравнение равносильно уравнению (4.3)
, то исходное уравнение равносильно уравнению (4.3)
Рассмотрим функции  ,
,  где
где  и
и  .
.
1. Графиком функции  , где
, где  , является часть прямой, проходящей через точки А (–3; 2) и В (5; 10).
, является часть прямой, проходящей через точки А (–3; 2) и В (5; 10).
2. Графиком семейства функций 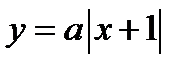 является «подвижный уголок» с неподвижной вершиной в точке С (–1; 0) и подвижными сторонами
является «подвижный уголок» с неподвижной вершиной в точке С (–1; 0) и подвижными сторонами

3. Найдём при каких значениях параметра а график функции 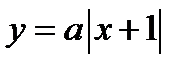 проходит через точку А (–3; 2) и определим сколько решений имеет исходное уравнение в этом случае.
проходит через точку А (–3; 2) и определим сколько решений имеет исходное уравнение в этом случае.
 а) График функции
а) График функции 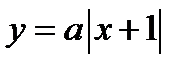 проходит через точку А (–3; 2), если
проходит через точку А (–3; 2), если 
б) Если  , то функция
, то функция 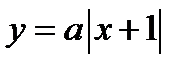 принимает вид
принимает вид  и на отрезке
и на отрезке  имеем
имеем
 в) Так как прямая
в) Так как прямая  параллельна прямой
параллельна прямой  , а прямая
, а прямая 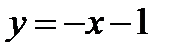 пересекает прямую
пересекает прямую  в точке А (–3; 2), то график функции
в точке А (–3; 2), то график функции  на отрезке
на отрезке  пересекает прямую
пересекает прямую  в одной точке А (–3; 2) (рис.11). Тогда исходное уравнение при
в одной точке А (–3; 2) (рис.11). Тогда исходное уравнение при  имеет единственное решение.
имеет единственное решение.
4. Найдём при каких значениях параметра а график функции
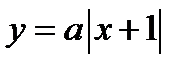 проходит через точку В (5; 10) и определим сколько решений имеет исходное уравнение в этом случае.
проходит через точку В (5; 10) и определим сколько решений имеет исходное уравнение в этом случае.
а) График функции 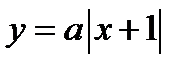 проходит через точку В (5; 10), если
проходит через точку В (5; 10), если 
б) Если  , то функция
, то функция 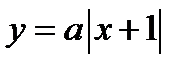 принимает вид
принимает вид  и на отрезке
и на отрезке  имеем
имеем

в) Точку пересечения прямых  ,
,  , где
, где  найдём из системы
найдём из системы

Прямые  ,
,  пересекаются на отрезке
пересекаются на отрезке  в точке С (–2,5; 2,5).
в точке С (–2,5; 2,5).
г) Точку пересечения прямых  и
и  , где
, где  найдём из системы
найдём из системы

Прямые  ,
,  на промежутке
на промежутке  пересекаются в точке В (5; 10).
пересекаются в точке В (5; 10).
д) График функции  на отрезке
на отрезке  пересекает прямую
пересекает прямую  в двух точках: В (5; 10), С (–2,5; 2,5) (рис.11).
в двух точках: В (5; 10), С (–2,5; 2,5) (рис.11).
Исходное уравнение при  имеет два решения.
имеет два решения.
Из рисунка (рис.11) для  и замечания следует ответ.
и замечания следует ответ.
Ответ. Если  , то нет решений; если
, то нет решений; если  , то одно решение; если
, то одно решение; если  , то два решения.
, то два решения.
Замечание. Графический метод даёт наглядную интерпретацию решения задачи. С помощью этого метода может быть получен ответ наглядно и быстро, но очень часто только графическая интерпретация оказывается недостаточной и для полного обоснования требуются дополнительные исследования.
5. При каких значениях параметра  уравнение
уравнение  имеет единственный корень; имеет два корня; не имеет корней?
имеет единственный корень; имеет два корня; не имеет корней?
Решение. 1. Рассмотрим функции  где
где  . Построим графики функций
. Построим графики функций  и
и  при
при  (областью определения функции
(областью определения функции  является интервал
является интервал  ).
).
Графиком функции  , где
, где  является «уголок» с вершиной в точке А (2; 1) и сторонами
является «уголок» с вершиной в точке А (2; 1) и сторонами


Функция  для каждого значения параметра а задаёт семейство логарифмических функций,проходящих через точку В (1; 0).
для каждого значения параметра а задаёт семейство логарифмических функций,проходящих через точку В (1; 0).
 На рисунке 12 а) изображён график функции
На рисунке 12 а) изображён график функции  , где
, где  а на рисунке 12 б) изображён график функции
а на рисунке 12 б) изображён график функции  , если
, если  , при некоторых значениях параметра
, при некоторых значениях параметра  .
.
2. Если график функции 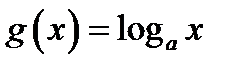 проходит через точку А (2; 1), то он может пересекать график функции
проходит через точку А (2; 1), то он может пересекать график функции  в одной точке А (2; 1) или в двух точках (одна из этих точек А (2; 1)). В этом случае исходное уравнение имеет одно или два корня.
в одной точке А (2; 1) или в двух точках (одна из этих точек А (2; 1)). В этом случае исходное уравнение имеет одно или два корня.
График функции  проходит через точку А (2; 1), если
проходит через точку А (2; 1), если

При 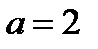 исходное уравнение принимает вид
исходное уравнение принимает вид
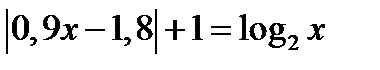 (5.1)
(5.1)
3. Уравнение (5.1) равносильно совокупности уравнений
 (5.2)
(5.2)
1) Рассмотрим первое уравнение совокупности (5.2).
Так как функция 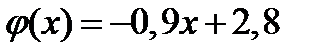 убывает, а функция
убывает, а функция  возрастает, то графики функций пересекаются только в одной точке – это точка (2; 1), а тогда уравнение (5.1) при
возрастает, то графики функций пересекаются только в одной точке – это точка (2; 1), а тогда уравнение (5.1) при  , а значит и исходное уравнение при
, а значит и исходное уравнение при 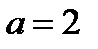 и
и  , имеет единственный корень:
, имеет единственный корень:  .
.
2) Рассмотрим второе уравнение совокупности (5.2).
Найдём число точек пересечений графиков функций 
 при
при 
Рассмотрим функцию

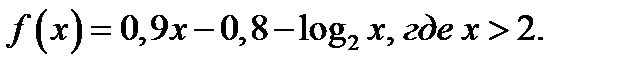
Найдём промежутки монотонности функции  .
.
а) Найдём производную функции  . Имеем
. Имеем

б) Определим знак 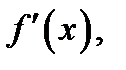 если
если 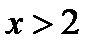
Так как  , то
, то  . Так как функция
. Так как функция  убывает, если
убывает, если  то
то  , а тогда
, а тогда 
Таким образом,  если
если 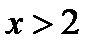 . Тогда функция
. Тогда функция  возрастает на интервале
возрастает на интервале 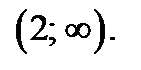
Так как  и функция
и функция  возрастает на интервале
возрастает на интервале  , то
, то
 (5.3)
(5.3)
Из системы (5.3) следует: графики функций  и
и
 не пересекаются при
не пересекаются при  . Это означает, что уравнение (5.1) при
. Это означает, что уравнение (5.1) при 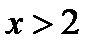 , а значит и исходное уравнение при
, а значит и исходное уравнение при 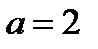 и
и 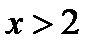 не имеет корней.
не имеет корней.
Из 1) и 2) следует, что уравнение (5.1), а значит и исходное при 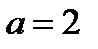 , имеет единственный корень.
, имеет единственный корень.
4. Построим графики функций  и
и  при
при  и
и  . Для этого воспользуемся следующим: так как
. Для этого воспользуемся следующим: так как  то найдётся такое значение
то найдётся такое значение 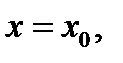 что для всех
что для всех 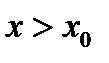 выполняется неравенство
выполняется неравенство 
На рисунке 12 в) изображены графики функций 

 если
если  и
и  .
.






