В1. Найдите наибольшее значение функции 
на 
.
В2. Через точку (1;-3) проходят две касательные к графику функции 
. Найдите сумму ординат точек касания.
В3. При каком наибольшем целом значении m функция 
убывает на всей числовой прямой.
Запишите решение заданий уровня С с полным обоснованием
С1. При каких значениях а уравнение 
не имеет корней.
С2. При каком значении а прямая 
является касательной к графику функции 
.
Диагностическая контрольная работа
По алгебре и началам анализа
«Производная функции. Приложения производной»
Вариант 28
Запишите вариант правильного ответа заданий уровня А
А1. Найти y ´(-3), если y = x 3(2 x 2-3).
| а) 324 | б) 729 | в) 405 | г) 891 |
А2. Найти 
, если 
.
а) 
| б) 
| в) 
| г)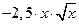 
|
А3. Вычислить 
для функции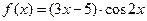 
.
| а) 0 | б) 3 | в) 
| г) 
|
А4. Найти минимум функции 
.
| а) 6 | б) 5 | в) 4 | г) 3 |
А5. Найти сумму длину промежутка (промежутков) возрастания функции 
.
| а) 4 | б) 3 | в) 2 | г) 1 |
А6. К графику функции 
проведена касательная в точке N (-1;4). Найдите угловой коэффициент касательной.
| а) -2 | б) -1 | в) 1 | г) 2 |
А7. Выберите уравнение касательной к графику функции 
, если касательная проходит через точку (0;0) и абсцисса точки касания положительна.
а) 
| б) 
| в) 
| г) 
|
А8. Точка движется по координатной прямой по закону 
. Определите координату точки в момент времени, когда скорость движения равна 2.
| а) 12 | б) 2 | в) 3 | г) 4 |
А9. Дан график функции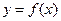 
. Найти значения х, при которых 
.
а) 
| б) 
|
в) 
| г) 
|
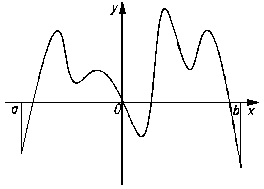А10. Дан график 
на [a;b]. Определите количество точек максимума функции .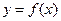
| а) 4 | б) 3 |
| в) 2 | г) 1 |
А11. Дан график функции 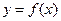на отрезке [-4;6]. Определите количество критических точек функции 
.
| а) 5 | б) 4 |
| в) 3 | г) 1 |
А12. Решите уравнение 
, если 
, 
, 
.
| а) 0,4 | б) 0,8 | в) 3,8 | г) 5,6 |
