В1. При каких значениях аргумента касательная к графику функции 
будет составлять с положительным направлением оси абсцисс угол 45°? (записать сумму аргументов)
В2. Найдите наибольшее значение функции 
на отрезке [1;9].
В3. Каковы должны быть стороны прямоугольного участка, периметр которого равен 120 м, чтобы площадь этого участка была наибольшей? (записать в ответе площадь участка)
Запишите решение заданий уровня С с полным обоснованием
С1. При каких значениях параметра в уравнении 
имеет ровно два корня?
С2. На графике функции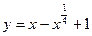 
найдите точку, сумма расстояний от которой до осей координат наименьшая.
Диагностическая контрольная работа
По алгебре и началам анализа
«Производная функции. Приложения производной»
Вариант 24
Запишите вариант правильного ответа заданий уровня А
А1. Найдите производную функции: f (x)=15 x 5-13 x
| а) f ′(x)=75 x 5-13 | б) f ′(x)=15 x 6-13 x 2 | в) f ′(x)=75 x 4-13 | г) f ′(x)=75 x 5-13 x |
А2. Найдите скорость изменения функции y =3 x -7
| а) -7 | б) 3 | в) -4 | г) -10 |
А3. Найдите значение производной в точке x 0, если g(x)=sin x, 
а) 
| б) 
| в) 
| г) 
|
А4. Для какой из функций производная задается формулой y ′= cosx -20 x 3?
| а) y = cosx -5 x 4 | б) y = sinx -20 x 4 | в) y =- sinx -5 x 4 | г) y = sinx -5 x 4 |
А5. Определите промежутки в которых производная функции y = g (x) принимает отрицательные значения, если данные о функции y = g (x) указаны в таблице.
| X | 
| -12 | (-12;-3) | -3 | (-3;5) | 
| |
| g | 
| 
| -1 | 
|
| ||
а) 
| б) 
| в) 
| г)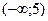 
|
А6. Найдите угловой коэффициент касательной к графику функции y =5 cosx -3 sinx в точке 
| а)
| б) 
| в) 
| г) 
|
А7. Тело движется по прямой, так что расстояние S от начальной точки изменяется по закону S =6 t -1,5 t 2 (м), где t - время в секунду. Найдите скорость тела через 1 с после начала движения.
| а) 4,5 м/с | б) 3 м/с | в) 7 м/с | г) 9 м/с |
А8. Дана функция 
. Найдите точки ее графика в которой угловой коэффициент касательной к нему равен 2.
| а) (6;-4) | б) (6;0) | в) (2;-4) | г) (2;-8) |
А9. Тело движется по прямой, так что расстояние S от начальной точки изменяется по закону S =5 t -1,5 t 2 (м). В какой момент времени скорость будет равняться 3.
| а) t =2 c | б) t =5 c | в) t =7 c | г) t =2/3 c |
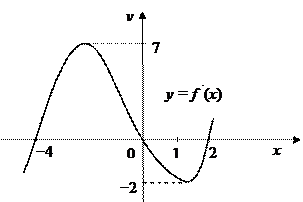А10. На рисунке изображен график производной функции y = f ′(x). Найдите точку максимума функции y = f (x)
а) -4
б) -2
в) 0
г) 2
А11. Найдите производную функции 
| а) f ′(x)=- cosx | б) f ′(x)= cosx | в) f ′(x)=- sinx | г) иной ответ |
А12. Найдите график производной по графику функции y=f (x)
| а) 1 | б) 2 | в) 3 | г) 4 |
