В1. Сумма двух целых чисел равна 24. Найдите эти числа, если известно, что их произведение принимает наибольшее значение.
В2. Найти производную функции  в точке
в точке 
В3. Решите уравнение: 
Запишите решение уровня С с полным обоснованием
С1. Найти область значения функции  на интервале
на интервале 
С2. При каких значениях параметра  касательные к графику функции
касательные к графику функции 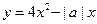 , проведенные в точках его пересечения с осью ОХ, образует между собой угол 600.
, проведенные в точках его пересечения с осью ОХ, образует между собой угол 600.
Диагностическая контрольная работа
По алгебре и началам анализа
«Производная функции. Приложения производной»
Вариант 16
Запишите вариант правильного ответа заданий уровня А
A1. Найти производную функции 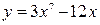
a) 
| б) 
| в) 
| г) 
|
A2. Определите скорость изменения функции  ,
, 
а) 2 б) 4 в) -8 г) -4
А3. Решить неравенство 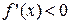 , если
, если 
а)  б)
б)  в)
в)  г)
г) 
A4. На рисунке изображен график производной функции 
|
|

Найти точки максимума функции 
а) -4 б) 0 в) -2 г) 4
А5. Среди заданных функций укажите ту, производная которой имеет вид

а)  б)
б)  в)
в)  г)
г) 
A6. При движении тела по прямой расстояние S от начальной точки движения изменится по закону  . Найдите скорость тела через 4 секунды после начала движения
. Найдите скорость тела через 4 секунды после начала движения
а) 1,75 б) 7,5 в) 3 г) 9
А7. Найдите наименьшее значение функции  на отрезке [0;3]
на отрезке [0;3]
а) 0 б) -4 в) -2 г) 2
А8. Найдите промежутки убывания функции 
а) (1;5) б) [0;9] в) [3;12] г) (3;15]
A9. Вычислите значение производной функции  в точке
в точке  .
.
а) 
| б) 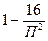
| в) 
| г) 
|
А10. Написать уравнение касательной к графику функции  в точке с ординатой
в точке с ординатой 
а)  б)
б)  ,
,
в)  г)
г) 
А11. Найдите количество точек экстремума функции 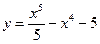
а) 1 б) 3 в) 2 г) 0
А12. К графику функции  в точке с абсциссой
в точке с абсциссой  проведена касательная. Найдите ординату точки касательной, абсцисса которой равна 11
проведена касательная. Найдите ординату точки касательной, абсцисса которой равна 11
а) 34 б) 35 в) 32 г) 33






