а) 
| б) (2+3х) | в)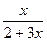 
| г)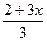 
|
Запишите решение заданий уровня В с полным обоснованием
В1. Задайте формулой функцию, если 
.
В2. Найдите интервалы возрастания и убывания функции 
.
В3. Найти точки графика функции f(x), в которых касательная к этому графику параллельна прямой y=kx.
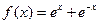, k = 
.
Запишите решение заданий уровня С с полным обоснованием
С1. При каком значении параметра а функция 
имеет минимум в точке x 0 = 1?
С2. При каких значениях параметра a функция 
возрастает на всей числовой прямой.
Диагностическая контрольная работа
По алгебре и началам анализа
Тема «Производная функции. Приложения производной»
Вариант 14
Запишите вариант правильного ответа заданий уровня А
А1. Найти производную функции 
.
а) 
| б)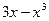 
| в)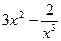 
| г) 
|
А2. Тело движется по закону 
определить скорость тела в момент времени t = 10.
| а) 20 | б) 12 | в) 27 | г) 22 |
А3. Вычислить значение производной функции 
при 
.
а) 
| б) 0 | в) -
| г) 
|
А4. Найти значения производной при заданном значении аргумента 
при x 0 =2.
| а) 11 | б) 8 | в) 2 | г) 3 |
А5. Решить уравнение 
, если 
.
| а) -0,2 | б) 0,2 | в) 0 | г) 5 |
А6. Найти производную функции 
.
а) 
| б) 
| в) 
| г)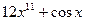 
|
А7. Решить уравнение 
.
а) 
| б) 
| в) 
| г) 
|
А8. Укажите производную функции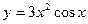 
.
а) 
| б) 
| в) 
| г)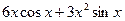 
|
А9. Найти тангенс угла наклона к оси абсцисс касательной, проходящей через данную точку M графика функции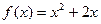 
, M (1;3).
а) 
| б) 
| в)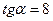 
| г) 
|
А10. Написать уравнение касательной к графику функции 
в точке с абсциссой х 0 =1.
а)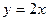 
| б) 
| в) y=0 | г) 2-х |
А11. Найти промежутки возрастания функции 
.
.
а) 
| б) 
| в) 
| г) 
|
А12. Найти производную функции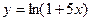 
.
а) 
| б) 
| в) 
| г) 
|
