В1. К графику функции y =  +
+ 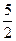 x 2- x проведите касательную так, чтобы она была параллельна прямой y =2- x
x 2- x проведите касательную так, чтобы она была параллельна прямой y =2- x
B2. На рисунке изображен график производной функции y = f ´(x), заданной на отрезке [ a; в ]. Исследуйте функции y = f (x) на монотонность и в ответе укажите число промежутков убывания.
 |
B3. Найдите наибольшее значение функции y =2 x 3-9 x 2+12 x -3 на отрезке [0;3]
Запишите решение заданий уровня С с полным обоснованием
C1. При каком значении а функция f (x)= x  имеет экстремум в точках x =-2 и x =2?
имеет экстремум в точках x =-2 и x =2?
C2 Решите графически уравнение x 3-3 x =(x +1)6+2
Диагностическая контрольная работа
По алгебре и началам анализа.
«Производная функции. Приложения производной»
Вариант 11
Запишите вариант правильного ответа заданий уровня А
А1. Найти производную функции  .
.
а) 
| б) 
| в) 
| г) 
|
А2. Найти производную функции f(x) = 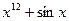 .
.
| а) 12x+cosx | б) 
| в) 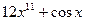
| г) 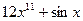
|
А3. Найти производную функцию  .
.
а) 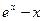
| б) 
| в) 
| г) 
|
А4. Вычислить  , если
, если  .
.
| а) 9 | б) 5+4е | в) 5 | г) -5+4е |
А5. Найти значение производной функции  в точке x 0 =π.
в точке x 0 =π.
а) 
| б)2π+1 | в)2 π-1 | г)2 π |
А6. Найти значение производной функции 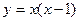 в точке x0=0.
в точке x0=0.
| а) 0 | б) 1 | в) -1 | г) 2 |
А7. Найти тангенс угла наклона касательной, проведенной к графику функции 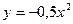 в его точке с абсциссой x0= -3.
в его точке с абсциссой x0= -3.
| а) -3 | б) -4,5 | в) 3 | г) 0 |
А8. Найти угловой коэффициент касательной, проведенной к графику функции  в его точке с абсциссой x 0=2.
в его точке с абсциссой x 0=2.
| а) 1 | б) -5 | в) -1 | г) 5 |
А9. Найти угловой коэффициент касательной, проведенной к графику функции  в его точке с абсциссой x 0=0.
в его точке с абсциссой x 0=0.
| а) 1 | б) 2 | в) 3 | г) 0 |
А10. Координата материальной точки изменяется с течением времени по закону  . Найдите скорость точки в момент времени t =6.
. Найдите скорость точки в момент времени t =6.
| а) 2 | б) 29 | в) 32 | г) 36 |
А11. Найдите значение производной функции  в точке x 0=0.
в точке x 0=0.
| а) 1 | б) 0 | в) 0,5 | г) -1 |
А12. Решите уравнение  , если
, если  .
.
а) 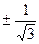
| б) 2 | в) 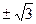
| г) 0 |




