Конусом второго порядка называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид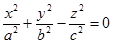 
, где 
- положительные числа.
С математической точки зрения поверхность лучше определять с помощью уравнения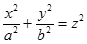 
, так как в нем меньше параметров, но при этом, во-первых, теряется аналогия с уравнениями предыдущих поверхностей, а во-вторых, если считать, что величины 
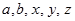имеют размерность длины, то в уравнении размерности правой и левой части не согласуются.
Для краткости в дальнейшем конус второго порядка будем называть просто конус. Исследуем форму конуса. Так же, как эллипсоид и гиперболоиды, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.
Для построения конуса найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью 
. На этой плоскости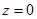 
, поэтому 
.
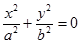Координаты только одной точки плоскости могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью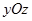 
. На этой плоскости 
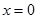, поэтому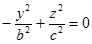 
Это уравнение пары прямых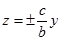 
на плоскости 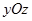. Построим эти прямые (рис.15). Сечение плоскостью 
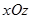также является парой прямых с уравнением 
.
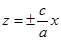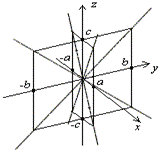
Рис. 15. Сечения плоскостям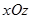и и .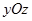
Найдем линии пересечения поверхности с плоскостями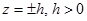 
. Уравнения этих линий
Первое уравнение преобразуем к виду 
. Обозначив 
и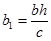 
, получим
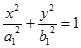
Данное уравнение является уравнением эллипса. Построим полученные сечения (рис. 17).
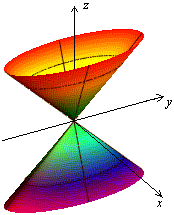
Рис.16. Дополнительное сечение Рис.17. Изображение конуса с помощью сечений
Точка пересечения конуса с плоскостью называется вершиной конуса.
Если в каноническом уравнении 
, то сечения конуса плоскостями параллельными плоскости являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости 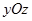, вокруг оси 
.
