Определение.
Поверхностью второго порядка называется поверхность, определяемая уравнением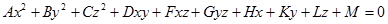 
, где A, B, C, D, F, G, H, K, L, M - вещественные числа, причем хотя бы одно из чисел A, B, C, D, F, G отлично от нуля.
Поверхности второго порядка, за исключением случаев сильного вырождения, можно разделить на пять классов: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением. Этот факт будет обоснован позже.
Сфера
Определение.
Сферой называется геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром.
Теорема Сфера радиуса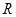 
с центром в точке 
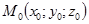имеет уравнение
.
Пример 1 Построить сферу, заданную уравнением 
.
Решение. Выделив полные квадраты, получим
.
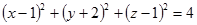Следовательно, центром сферы является точка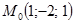 
, радиус сферы 
.
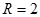Для ее изображения построим сечения сферы плоскостями, проходящими через центр и параллельными координатным плоскостям. Каждое такое сечение будет окружностью радиуса 2 с центром в точке 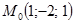(рис1).
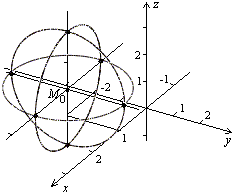
Рис.1. Рис.2.
