Рассмотрим случай:
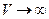
Влияние границы 
отсутствует.
, т.е. мы можем помещать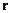 
и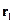 
в любое место пространства.
Получим Фурье-образ и саму функцию Грина. Рассматриваем случай изотропной среды.
Для удобства, временно примем обозначение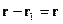 
.
Тогда:
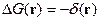
Запишем для 
и 
разложение в интеграл Фурье:
Здесь 
- фурье-образ, а 
- элементарный объём в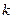 
-пространстве.
фурье-образ -функции равен 
Рассмотрим левую часть этого равенства. Лапласиан 
действует на 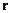, значит, нам надо рассчитать 
Т.е. переходит в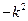 
, тогда получим:
тогда 
Переход в 
-пространство переводит дифференциальное уравнение в алгебраическое.
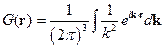
Этот интеграл можно взять, используя теорию вычетов. Получаем:
Производим обратную замену 
:
