Общее решение уравнения Пуассона  состоит из общего решения соответствующего однородного уравнения -
состоит из общего решения соответствующего однородного уравнения -  и частного решения неоднородного -
и частного решения неоднородного - 


На  лежит нагрузка удовлетворения граничным условиям,
лежит нагрузка удовлетворения граничным условиям,  удовлетворяет однородным граничным условиям:
удовлетворяет однородным граничным условиям:

Рассмотрим  . Далее будем писать
. Далее будем писать  без индекса, т.е.
без индекса, т.е.  .
.
Введём некоторый интегральный оператор  и
и
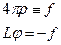
Если  , то
, то 
 - ядро интегрального оператора
- ядро интегрального оператора  , т. е.
, т. е.  - функция Грина.
- функция Грина.


Пусть  - единичный оператор, т.е.
- единичный оператор, т.е.  , тогда:
, тогда:


 -ядро единичного оператора, это и есть
-ядро единичного оператора, это и есть 
Итак,  на языке ядер выглядит следующим образом:
на языке ядер выглядит следующим образом:
 ,
,  есть функция Грина задач электростатики.
есть функция Грина задач электростатики.
 определяется характером граничных условий.
определяется характером граничных условий.
1.  - частное решение, удовлетворяющее однородному граничному условию Дирихле.
- частное решение, удовлетворяющее однородному граничному условию Дирихле.

тогда из того, что 
2.  - граничное условие Неймана
- граничное условие Неймана
В обоих случаях  и
и 
Для 







