Якщо при деякому  будь-яка із умов неперервності означення 20 не виконується, то кажуть, що функція в цій точці має розрив, а точку
будь-яка із умов неперервності означення 20 не виконується, то кажуть, що функція в цій точці має розрив, а точку  називають точкою розриву функції.
називають точкою розриву функції.
Розриви функції бувають ліквідовані та неліквідовані:
1) якщо функція  не визначена в точці
не визначена в точці  або визначена, але мають місця співвідношення
або визначена, але мають місця співвідношення 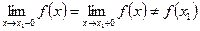 , то розрив в точці
, то розрив в точці  називають ліквідованим. В цьому випадку функцію можна визначити або замінити її значення в точці х1 так, щоб виконувалась рівність
називають ліквідованим. В цьому випадку функцію можна визначити або замінити її значення в точці х1 так, щоб виконувалась рівність  ;
;
2) неліквідовані розриви поділяються н розриви першого та другого роду:
a. Якщо однобічна границя  ,
,  існують та скінченні, але не рівні між собою, то х1 називають точкою розриву першого роду, а різницю
існують та скінченні, але не рівні між собою, то х1 називають точкою розриву першого роду, а різницю  називають стрибком функції;
називають стрибком функції;
b. Якщо хоч би одна з однобічних границь не існує або дорівнює  , то розрив в цій точці називають розривом другого роду.
, то розрив в цій точці називають розривом другого роду.






