Елементи матричного аналізу
Характеристики змінних величин
Поняття функції
Властивості функції
Область визначення та значення функції, заданої аналітично
Основні елементарні функції
Складні та елементарні функції
Характеристики змінних величин.
Означення 1. Величиною називають те, що можна виразити в певних одиницях та характеризувати числовим значенням.
Наприклад, площа та довжина кола – величина тому, що вимірюються в певних одиницях і характеризуються деякими числовим значенням. Коло не буде величиною, тому що для нього характерна лише певна форма.
Величини бувають розмірні та безрозмірні. Розмірністю величини називають ту одиницю, через яку величина виражається.
Наприклад, розмірність площі – см2, м2, км2.
Додавати та віднімати можна величини лише однакової розмірності. Множити та ділити величини можна будь-якої розмірності.
Наприклад, швидкість 10 км/год.
Якщо поділити дві величини однакової розмірності, то одержимо безрозмірну величину. Наприклад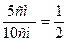 
.
В математиці найчастіше вивчають безрозмірні величини, які повністю характеризуються лише своїм числовим значенням.
Величини бувають постійні та змінні.
Означення 2. Величина, числове значення якої при розглядаємих умовах не змінюється, називається постійною.
Змінною величиною називається величина, яка при розглядаємих умовах може приймати різні числові значення.
До основних характеристик змінної величини відносяться: неперервністю або дискретність, монотонність, обмеженість (повна або часткова) або необмеженість.
Поняття функції.
Часто при дослідженні певного явища доводиться мати справи одночасно з деякою кількістю змінних величин. Наприклад, для виготовлення виробів кількістю у застосовують х сировини, z – палива і т.д.
Деякі з розглядаємих змінних можуть бути зв’язані одна з іншою так, що зміна однієї величини приводить до зміни іншої величини. В цьому випадку кажуть,що між цими величинами існує функціональна залежність.
Серед функціонально залежних величин можна вказати такі величини значення яких можна обирати довільно (ці величини називають незалежними змінними), тоді як значення інших величин визначають значеннями незалежних змінних (їх називають залежними величинами).
Наприклад, якщо розглядати зв’язок між величинами кормів х та надоїв у, тоді доцільно за незалежну змінну прийняти х, а надої 
буде залежною змінною.
Означення 2. Змінна величина у називається функцією змінної величини х, якщо вказано закон, за яким кожному значенню х, взятому з області можливих значень, відповідає певне дійсне значення у. Змінну величину х називають незалежною змінною або аргументом.
Якщо у є функцією х, то кажуть, що величини х та у зв’язані функціональною залежністю і позначають .
Означення 4. Функція називаються однозначною, якщо кожному значенню х відповідає одне значення у. Функцію у називають багатозначною, якщо кожному значенню х відповідає декілька значень у.
Існує декілька способів завдання функції: аналітичний, табличний, графічний, мовний та програмний. В математиці найбільш часто використовують перші три способи, тому детально їх розглянемо.
1. При аналітичному способі функція задається однією або декількома рівностями, що зв’язують залежні та незалежні змінні.
2. При табличному способі функціональна залежність задається у вигляді таблиці, в якій для кожного числового значення х вказано відповідне числове значення у.
3. Графічний спосіб найбільш наглядний і базується на застосуванні методу координат. При цьому способі функціональна залежність зображується лінією, яку називають графіком функції.
