Перша визначна границя.
При знаходженні границі виразів, що містять тригонометричні функції, часто використовувати границю
 ,
,
яку називають першою визначною границею.
Друга визначна границя.
Розглянемо послідовність  ,
,  та підрахуємо декілька її значень
та підрахуємо декілька її значень
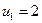 ;
; 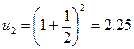 ;
;  ;
;  ;
; 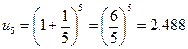 ;…
;…
Бачимо, що  . Можна довести, що для будь-якого n має місце нерівність
. Можна довести, що для будь-якого n має місце нерівність  яка означає, що зміна
яка означає, що зміна  монотонно зростає. В той же час усі підраховані значення
монотонно зростає. В той же час усі підраховані значення  задовольняють нерівність
задовольняють нерівність 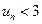 . Можна показати, що ця нерівність має місце для усіх значень n. Отже, зміннна
. Можна показати, що ця нерівність має місце для усіх значень n. Отже, зміннна  монотонно зростає і залишається обмеженою зверху числом 3. Згідно з другою ознакою існування границі змінної величини робимо висновок, що ця змінна
монотонно зростає і залишається обмеженою зверху числом 3. Згідно з другою ознакою існування границі змінної величини робимо висновок, що ця змінна  має скінченну границю.
має скінченну границю.
Означення. Скінченну границю послідовності  ,
,  називають числом е, тобто
називають числом е, тобто  .
.




