Волны, распространяющиеся в среде без источников, называются нормальными. Такие волны удовлетворяют уравнениям Максвелла в среде в отсутствие источников, из которых получается волновое уравнение.
Подействовав на второе уравнение оператором V х, а на третье - (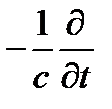
)получим:
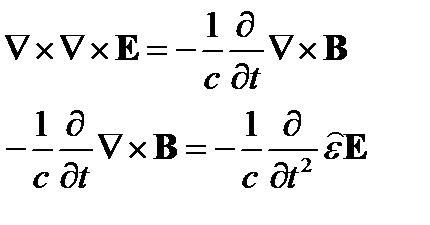
Сложив их, перейдем к волновому уравнению:
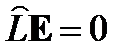
| (23) |
где 
Для плоской волны уравнение (23) принимает вид:
Введем фурье-образ L ядра 
здесь 
или в компонентах
Вместо (23) имеем:
Эта однородная система уравнений имеет нетривиальные решения лишь при условии 
или
| (24) |
Уравнение (24) называется дисперсионным. Оно устанавливает связь между 
и k: 
= 
(k).
Рассмотрим случай изотропной среды без пространственно- временной дисперсии:
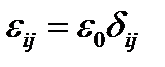
В терминах 
и 
тензор L имеет вид:
Тогда, приведя тензор 
к диагональному виду, получим:
Отсюда имеем:
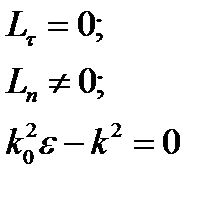
Окончательно получим:
где п - показатель преломления.
