Фронт волны - поверхность равных фаз.
Если фронт волны имеет вид плоскости, то она называется плоской.
- фронт волны;
- фазовая скорость, определяющая скорость движения фронта волны.
Рассмотрим случай электромагнитной волны, которая распространяется вдоль оси х: 
.
Обозначим через/любую компоненту векторов Е или Н, однако учтем, что:
Из волнового уравнения следует, что:
Но отличная от нуля компонента Ех означала бы наличие продольного электрического поля. Поскольку такое поле не имеет отношения к электромагнитной волне в вакууме, то можно положить Ех = 0.
Волновое уравнение перепишем в виде
| (13) |
Введем новые переменные:
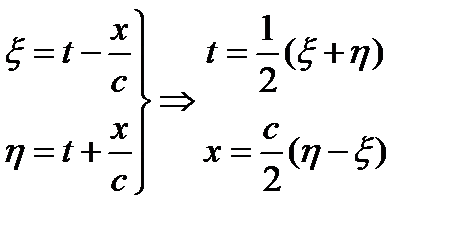
Тогда
и уравнение (13) для /принимает вид:
Отсюда для 
имеем:
Получили два решения, где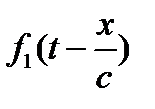 
- плоская волна, распространяющаяся в положительном направлении оси х, а 
- плоская волна, распространяющаяся в отрицательном направлении оси х.
Продифференцируем по 
Продифференцируем по 
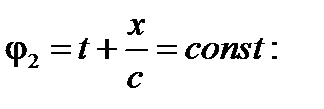
Рассмотрим случай 
Непрерывный спектр:
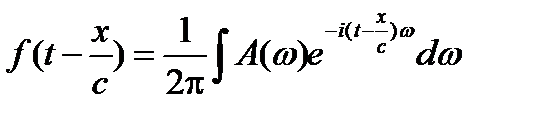
Дискретный спектр:
Выберем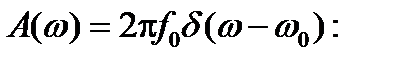 
Получим плоскую монохроматическую волну:
где 
групповая скорость, определяющая скорость переноса энергии.
Получим дисперсионное уравнение, соответствующее волновому уравнению:
| (14) |
Это дисперсионное уравнение, решение которого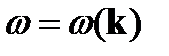 
. Из (14) имеем:
Из уравнений Максвелла для вакуума в отсутствие источников при подстановке Е и Н в виде плоской монохроматической волны
имеем:
Мы видим, что векторы Е и Н плоской волны направлены перпендикулярно направлению распространения волны. Поэтому электромагнитные волны называются поперечными. Причем вторая пара уравнений однозначно определяет взаимное расположение векторов k, Е и Н.
