Частные решения этих уравнений, полученные с помощью запаздывающей функции Грина, называются запаздывающими потенциалами. Для них (см. § 4) имеем:
| (11) |
Разложим потенциалы (И) в ряды по малому параметру. На рис.4
- оператор трансляции.
Тогда можно представить подынтегральные выражения в виде
| (12) |
где
Подставив (12) в (11), получим:
где 
= const;
Для калибровки Лоренца (6) получим:
Возьмем п = 0:
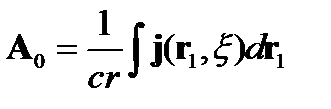
Докажем, что 
Уравнение непрерывности:
(правило суммирования Эйнштейна).
Первый интеграл равен нулю в силу теоремы Гаусса
так как на поверхности токи равны нулю. Далее
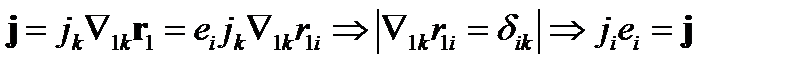
Тогда
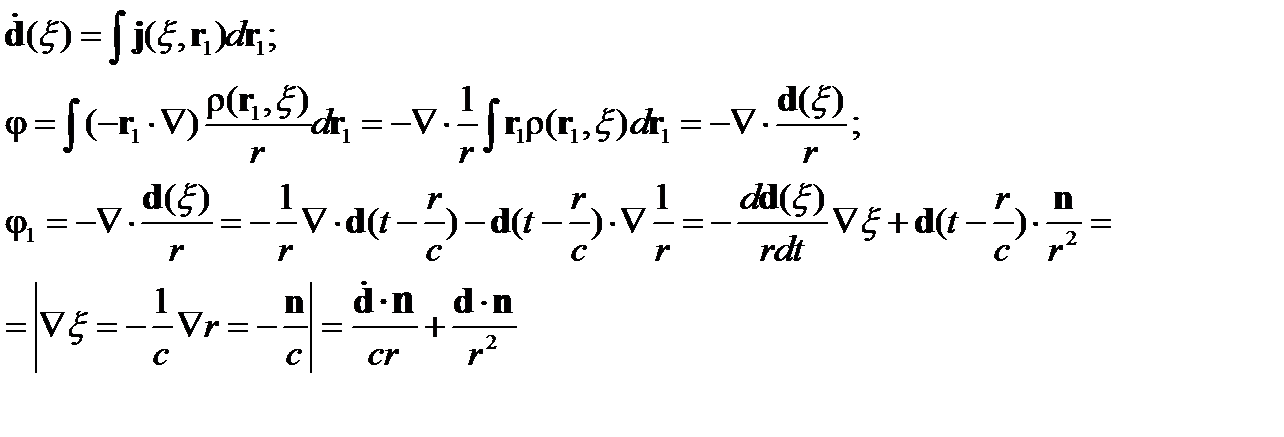
Подставим найденные значения для потенциалов в уравнение для калибровки Лоренца первого порядка 
Мы убеждаемся, что в этом порядке калибровка выполняется.
