При решении кристаллофизических задач часто оказывается удобной не кристаллофизическая (декартова система координат, условленным образом ориентированная относительно кристаллографической системы), а какая-то другая декартова система координат, направления осей которой определяются геометрией данной задачи. Так как система декартовых координат полностью задается своим ортонормированным базисом, преобразование декартовых координат означает переход от одного ортонормированного базиса к другому.
Преобразование, при котором ортонормированный базис переходит в ортонормированный, называется ортогональным преобразованием.
Пусть старая система координат 
построена на базисе 
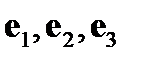, а новая 
-на базисе 
. Разложение нового базиса по векторам старого 
определяется коэффициентами 
, которые образуют матрицу ортогонального преобразования:
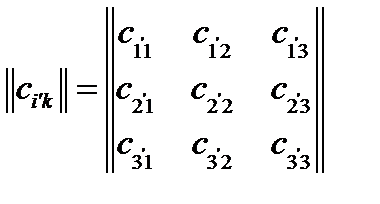
Она также называется матрицей косинусов, поскольку каждый ее элемент 
равен косинусу угла между соответствующими координатными осями. Ортогональные преобразования обладают тем свойством, что квадрат определителя их матрицы равен единице [4, с. 135].
Примерами матриц ортогональных преобразований могут выступать:
· матрица вращения вокруг оси Z:
· матрица отражения относительно плоскости XY:
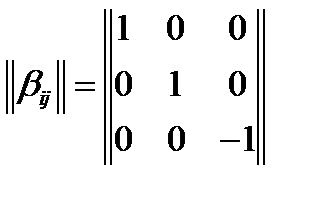
Для описания свойств кристалла введем материальные тензоры. Материальными называются тензоры, которые описывают свойства кристалла.
Пусть с кристаллом связана какая-либо декартова система координат. Набор компонент материального тензора относительно этой системы координат численно характеризует соответствующее свойство. Подвергнем координатную систему какому-либо ортогональному преобразованию. Компоненты материального тензора относительно новой системы, вообще говоря, не равны одноименным его компонентам относительно старой системы. Однако если данное преобразование входит в группу симметрии кристалла, то компоненты материального тензора относительно новой системы совпадают с его компонентами относительно старой. Следовательно, материальный тензор кристалла инвариантен относительно всех преобразований симметрии этого кристалла.
Пусть 
- материальный тензор, а 
- матрица преобразования симметрии кристалла, свойства которого этот тензор описывает. В новой системе координат
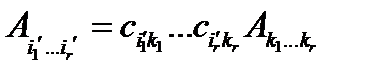
причем компоненты тензора в новой системе должны совпадать с его компонентами в старой системе. Поэтому можно записать:
Отсюда получим:
и эти 
равенств должны выполняться, если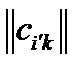 
- матрица преобразования симметрии.
