Электромагнитные волны в немагнитных анизотропных средах

 

Плоская монохроматическая волна. Распространение электро­магнитных волн в прозрачном немагнитном кристалле описывается уравнениями Максвелла в форме

 

(36)

 

и материальным уравнением

 

(37)

где E и D - векторы напряженности и индукции; с - скорость света в ва­кууме, а по повторяющемуся (немому) индексу к предполагается сум­мирование. Предположение о прозрачности кристалла приводит к от­брасыванию в полных уравнениях Максвелла источников поля (плот­ностей заряда и тока). Свойство немагнитности (пренебрежение намаг­ниченностью) кристалла выражается равенством Н = В.

Связь (37) между векторами Е и D осуществляется при помощи тензора диэлектрической непроницаемости ). Понятие тензора возни­кает при установлении линейных соотношений между внешним воз­действием и реакцией на него в анизотропных средах. Скалярная вели­чина (температура, энергия) представляется тензором нулевого ранга, векторная величина (напряженность и индукция электрического поля) - тензором первого ранга. Физические свойства кристаллов описываются тензорами разного ранга: нулевого (теплоемкость), второго (диэлек­трическая проницаемость) и т.п. Связь между индукцией и напряжен­ностью электрического поля

определяет тензор диэлектрической проницаемости , связанный с из (37) равенством

 

 

(38)

 

Тензоры 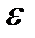и обладают свойством симметрии относительно переста­новки индексов

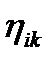Следует иметь в виду, что компоненты и тензоров и зави­сят, как и проекции , и векторов D и Е, от выбора системы коор­динат (базиса).

Если переменное электромагнитное поле распространяется в кри­сталле в форме плоской монохроматической волны, то для полей D, Е, Н будем иметь:

 

(39)

 

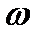где - фазовый множитель; - фаза волны; - волновой вектор; - циклическая частота. Равенство

 

(40)

 

определяет форму фронта волны - поверхности равной фазы. Легко ви­деть, что (40) представляет уравнение плоскости, нормаль к которой (волновая нормаль) - вектор . Можно показать, что имеют место соот­ношения

 

 

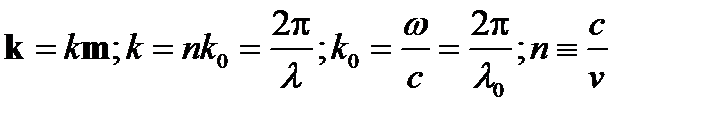
(41)

 

где - фазовая скорость света в рассматриваемой среде; п - показатель преломления среды, зависящий от направления единичного вектора волновой нормали m; 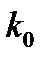- волновое число в случае вакуума, когда п = 1; и - длина волны света в среде и вакууме соответственно.

Пространственно-временная зависимость (39) полей D, Е и Н в случае плоской монохроматической волны существенно упрощает

уравнения (36), поскольку действие операторов и 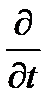на поля D, Е, Н

сводится к их действию на скалярную функцию . Это дает:

В силу этого для полей вида (39) устанавливается соответствие

 

(42)

 

С учетом (42) уравнения (36) в случае (39) принимают вид:

 

(43)

 

 

Отсюда следует, что поля D, Е, Н имеют одинаковую фазу , причем векторы k, D, H ₀ взаимно ортогональны, а Е ₀ в общем случае ортого­нален лишь вектору Н ₀. Таким образом, поперечность электромагнит­ных волн в анизотропных средах сводится к тому, что векторы D ₍₎ и

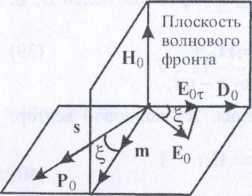
Н ₀ лежат в плоскости волнового фронта. Общий случай пространст­венного расположения векторов m, k, D ₍₎, H ₍₎ и Е ₀, удовлетворяющих (41) и (43), изображен на рис.9.

Исключив из пары векторных уравнений (43) поле Н ₀ и поделив на , получим уравнение

которое после преобразования двойного векторного произведения при­нимает вид:

 

(44)

 

где - составляющая поля , лежащая в плоскости волнового фронта (см. рис.9).

Воспользовавшись материальным уравнением (37) и введя в рас­смотрение поляризацию вектора D ₀ (единичный вектор в направлении исследуемого поля)

,

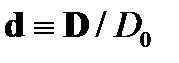вместо (44) запишем:

 

 

(45)

Векторному уравнению (45) соответствуют три (по числу проек­ций) скалярных:

 

(46)

Уравнение (45) позволяет по известным оптическим свойствам среды (тензор ) рассчитать соответствующие им значения показателя

преломления п, а также векторы d для волн, распространяющихся в кристалле в направлении m.

Действительно, представив (46) в форме

 

 

(47)

 

 

придем к системе однородных линейных уравнений относительно неиз­вестных . Критерий

существования нетривиального решения системы (47) сводится к квадрат­ному уравнению относительно (дисперсионному уравнению). Это озна­чает, что в общем случае существует не более двух различных значений , обозначаемых посредством 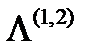.Им соответствуют два значения показателя преломления - и два значения фазовой скорости - .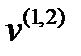

Подставив

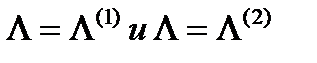
в матрицу и решив систему (47) вместе с условием нормировки

d² = 1, найдем поляризации и 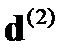обеих мод плоской монохромати­ческой волны поля D.

Можно показать, что и 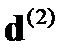ортогональны. С учетом вытекаю­щей из (43) ортогональности m и заключим: m, , 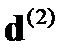взаимно ор­тогональны подобно m, D ₀, Н ₀. В случае, когда D ₀ коллинеарен вектору d ₀ = const, волна называется линейно-поляризованной.

Итак, при прохождении света через анизотропную среду в общем случае имеет место двойное лучепреломление - раздвоение луча, обус­ловленное зависимостью показателя преломления от поляризации d и направления m распространения волны. Проходящая через кристалл волна (39) распадается на две линейно-поляризованные волны, для ко­торых имеем:

(48)

В любой оптически анизотропной среде существуют особые на­правления - оптические оси, - вдоль которых раздвоения луча не проис­ходит. По числу (не более двух) этих осей кристаллы подразделяются на одноосные и двухосные.

Оптическая индикатриса. Задача нахождения и может быть проиллюстрирована геометрическими построениями, опирающи­мися на использование характеристической поверхности

(49)

тензора , называемой оптической индикатрисой (или эллипсоидом Пуансо).

 

 

Приведение поверхности (49) второго порядка к каноническому виду (или, что то же самое, приведение матрицы [ ] к диагональному виду) дает:

(50)

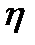где , - собственные (главные) значения , соответственно. Главные оси индикатрисы (50) ортогональны. Длины ее полуосей именуемые главными показателями преломления, - характерные пара­метры вещества. Напомним, что они зависят от частоты колебаний электромагнитного поля (39). В таблице приведены некоторые данные о форме оптической индикатрисы и свойствах кристаллов.

Форма оптической индикатрисы	Соотношение между	Оптические свойства кристаллов
Сфера		Изотропные
Эллипсоид вращения		Одноосные
Трехосный эллипсоид		Двухосные

 

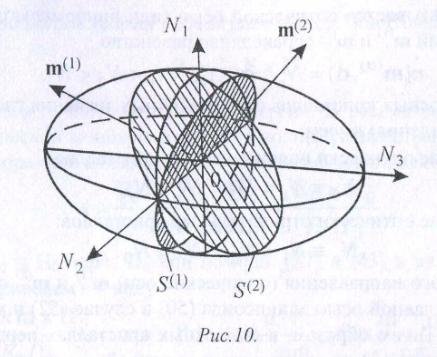
На рис. 10 изображена оптическая индикатриса двухосного кри­сталла вместе с характерными плоскостями и осями.

Центральным сечением называется кривая, получаемая от пересе­чения с оптической индикатрисой плоскости волнового фронта, прохо­дящего через начало координат (точку 0 на рис. 10). В общем случае эта кривая - эллипс, все точки которого удовлетворяют одновременно и уравнению индикатрисы, и уравнению плоскости волнового фронта. Если по известному вектору m нормали к фронту волны провести через точку 0 ортогональную ему плоскость, то длины 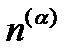полуосей цен­трального сечения, соответствующего данному m, представляют пока­затели преломления, определяющие, согласно (48), фазовые скорости обеих линейно-поляризованных волн, распространяющихся в направле­нии m.

У оптически изотропных кристаллов (см. таблицу) индикатриса - сфера и все центральные сечения - окружности. Это означает, что пока­затель преломления (48) не зависит ни от направления m распростране­ния волны, ни от ее поляризации d:

 

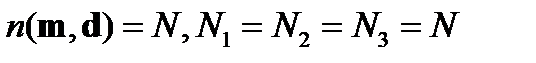
(51)

 

Равенство вида (51) имеет место и для оптически анизотропных веществ, но лишь для одного (одноосные кристаллы) или двух (двухос­ные кристаллы) направлений вектора m. Направление нормали , для которого центральное сечение (см. плоскость 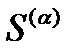на рис. 10) -

окружность, называется оптической осью (или бинормалью). На рис. 10 для направлений и справедливо равенство

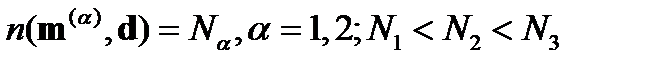
Для одноосных кристаллов (два различных значения главных пока­зателей преломления) имеем:

в случае оптически положительных кристаллов:

(52)

в случае оптически отрицательных кристаллов:

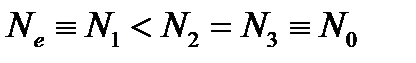
(53)

Вследствие этого направления (оптические оси) 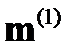и совпадают с большой () главной осью эллипсоида (50) в случае (52) и малой () - в случае (53). Таким образом, в одноосных кристаллах первый показа­тель преломления (53) не зависит от m, а второй - в разных направле­ниях различен. Первый показатель называют обыкновенным и обозна­чают 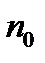; второй - необыкновенным и обозначают , его значения зависят от направления распространения волны.

Фазовая и групповая скорости. В анизотропных средах векторы и Е ₀ в общем случае неортогональны, поэтому возникает необходи­мость введения, наряду с вектором m, нормали к фронту волны другого единичного вектора s (называемого лучевым, или лучом), ортогональ­ного векторам Е ₀ и Н ₀ (см. рис.9).

Вектор m задает направление перемещения фронта волны, т.е. на­правление фазовой скорости. По определению,

где величина фазовой скорости v находится из условия постоянства фазы для точек фронта волны. Продифференцировав обе части равенства (40), получим:

Отсюда с учетом (37), (38) и (41) найдем:

Важную роль в теории поля играет вектор Пойтинга

имеющий смысл плотности потока энергии. В рассматриваемом случае (39), (43) плоской монохроматической волны, распространяющейся в оп­тически прозрачной анизотропной среде, для лучевого вектора имеем:

Выразив Е ₀ и Н ₀ через D ₀ при помощи (37) и (43) и введя единичный вектор d, приведем s к виду

Отсюда с учетом ортогональности векторов и (45) найдем:

Таким образом, угол между векторами D ₀ и Е ₀ равен углу между векто­рами m и s.

Для описания процесса переноса энергии электромагнитной волны вводится вектор групповой скорости u. Его направление совпадает с на­правлением s. В рассматриваемом случае прозрачных немагнитных кри­сталлов фазовая и групповая скорости связаны равенством

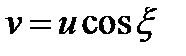
(54)

 

В общем случае для групповой скорости имеем:

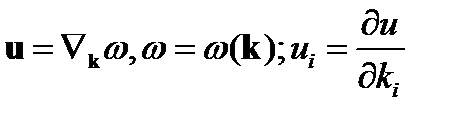
Для расчета необходимо знать решение дисперсионного уравнения типа (24).

В качестве альтернативного часто используется метод, основанный на принципе перестановочной двойственности, который в нашем случае сводится к следующему:

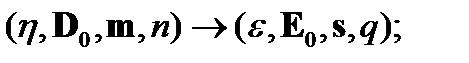
(55)

замена (55), осуществленная в соотношениях для волн, переводит их в соотношение для лучей (и обратно).

Замена (55), выполненная в (50), приводит к уравнению

характеристической поверхности тензора (в главных осях), име­нуемой эллипсоидом Френеля. Главные оси взаимно-обратных (38) тен­зоров и совпадают, однако длины соответствующих полуосей вза- имно-обратны. Построения на эллипсоиде Френеля идентичны построениям на индикатрисе (эллипсоиде Пуансо). Направления, пер­пендикулярные круговым сечениям эллипсоида Френеля, называются лучевыми оптическими осями, или бирадиалями. У одноосных кристал­лов бирадиали совпадают с бинормалями, а у двухосных лежат вместе с ними в плоскости оптических осей, которая ортогональна средней () главной оси обоих эллипсоидов.

По заданному лучу s рассчитываются, подобно (47), (48), пара­метры луча:

 

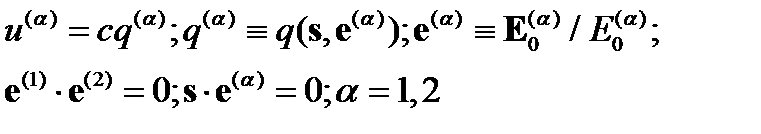
(56)

 

Из (48),(54) и (56) следует

В заключение еще раз отметим, что оптические свойства крис­таллов в значительной мере определяются свойствами симметрии тен­зоров и и геометрией соответствующих им квадратичных форм.