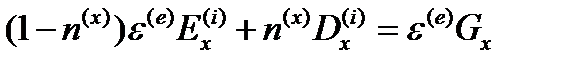Вначале рассмотрим некоторый частный случай - диэлектрический шар во внешнем постоянном поле G. Будем обозначать величины внутри шара индексом (i), а вне - (е). Выберем начало сферической системы координат в центре шара, причем азимутальный угол  будем отсчитывать от направления G. Будем искать потенциал вне шара в виде
будем отсчитывать от направления G. Будем искать потенциал вне шара в виде
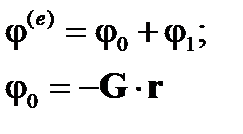
где 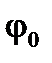 - потенциал внешнего приложенного поля, а
- потенциал внешнего приложенного поля, а 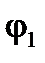 - изменение потенциала, вызванное шаром.
- изменение потенциала, вызванное шаром.
Потенциал как внутри, так и вне шара должен удовлетворять уравнению Лапласа в сферических координатах:
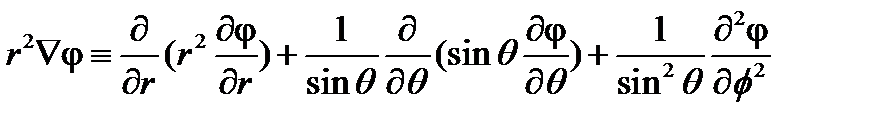
| (29) |
Найдем частные решения этого уравнения. Наложим ограничения для потенциала внутри шара - конечность во всем объеме шара, для потенциала вне шара - искажение потенциала, вызванное шаром на бесконечности, равно нулю.
Будем искать решение этого уравнения в виде

Так как рассматриваемое тело имеет шаровую симметрию, а внешнее поле - осевую, то

Тогда
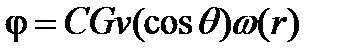
Подставив это решение в уравнение (29), получим:

Разделив переменные, получим:
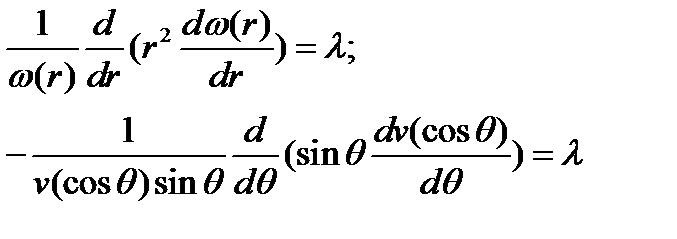
| (30) (31) |
Для уравнения (30) имеем:
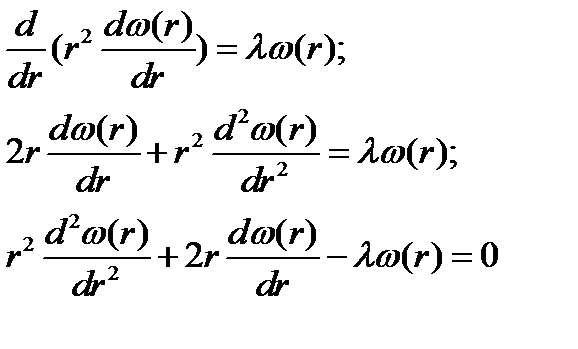
Таким образом, мы получили уравнение Эйлера. Для его решения используем стандартную замену переменных: 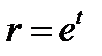 . Это дает:
. Это дает:

Корни характеристического уравнения имеют вид:
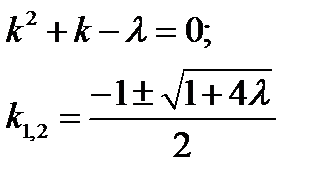
Наложив на решение упомянутые выше ограничения, получим:
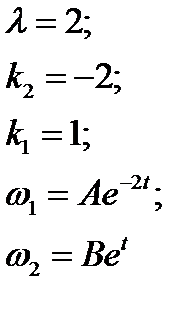
Сделаем обратную замену переменных 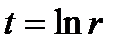 :
:
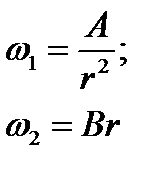
Найдем функцию  из уравнения (31) при
из уравнения (31) при 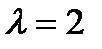 :
:

Видно, что этому уравнению удовлетворяет решение

Тогда

Здесь знак учитывает направление поля внутри шара в соответствии с направлением внешнего поля, так как 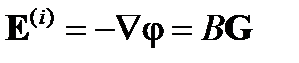 .
.
Постоянные А и В находятся из граничных условий:

Применив правила действия оператора 
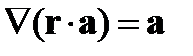
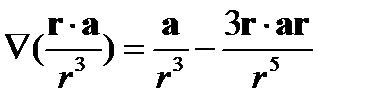
[5, с. 174], найдем при 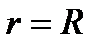 , где R - радиус шара,
, где R - радиус шара,
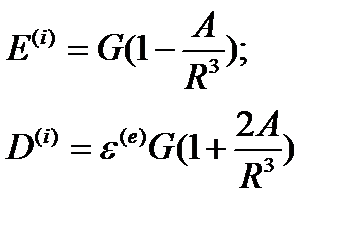
Выразим Аиз одного уравнения и подставим в другое:

Отсюда получим:
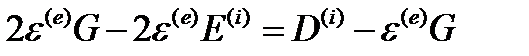
Теперь мы можем перейти к векторному равенству:

Подставим 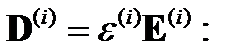

Рассмотрим случай бесконечного цилиндра в постоянном поле, перпендикулярном его оси. Потенциал вне цилиндра так же разобьем на две части: внешнего поля и искажения, вызванного цилиндром.
Выберем цилиндрическую систему координат, центр которой находится на оси цилиндра.
Тогда потенциал должен удовлетворять уравнению
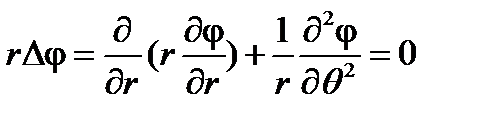
| (32) |
Найдем его в виде
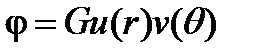
Действуя так же, как в первом случае, подставим это решение в уравнение (32)
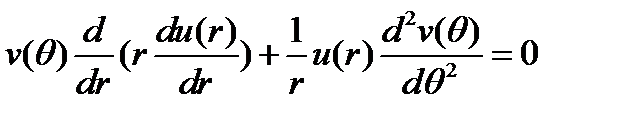
и разделим переменные
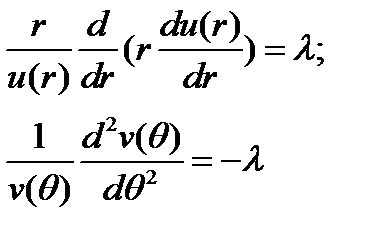
| (33) (34) |
Из(33) получим:
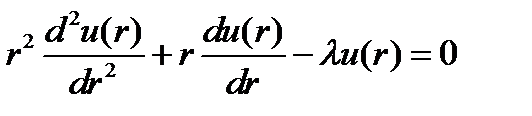
Применив стандартную замену переменных в уравнении Эйлера при 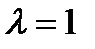 , получим два частных решения, удовлетворяющих условию конечности во всем объеме цилиндра и равенству нулю на бесконечности:
, получим два частных решения, удовлетворяющих условию конечности во всем объеме цилиндра и равенству нулю на бесконечности:

Решением уравнения (34) при 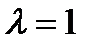 будет
будет 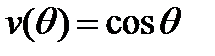 . Тогда потенциалы представим в виде
. Тогда потенциалы представим в виде
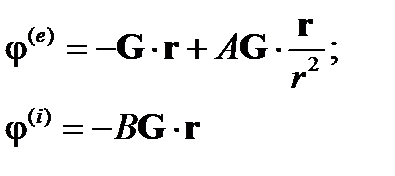
Так же, как и в случае шара, из граничных условий получим:

Выразив А из первого уравнения, подставим его во второе:
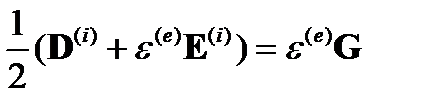
Это дает:

Перейдем непосредственно к случаю диэлектрического эллипсоида. Для нахождения поля внутри эллипсоида воспользуемся найденной нами закономерностью. Предположим, что эллипсоид находится в пустоте
(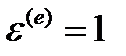 ) и все три вектора Е, D, G имеют направление вдоль оси х. Тогда, как и в вышеописанных случаях, существует связь:
) и все три вектора Е, D, G имеют направление вдоль оси х. Тогда, как и в вышеописанных случаях, существует связь:
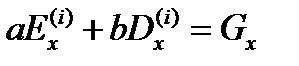
Для нахождения а и b воспользуемся двумя тривиальными случаями:
если 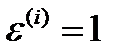 , то Е = D = G, отсюда а + b=1;
, то Е = D = G, отсюда а + b=1;
если эллипсоид проводящий, т.е.  , то индукция внутри эллипсоида не имеет непосредственного физического смысла, но может рассматриваться как формальная величина такая, что:
, то индукция внутри эллипсоида не имеет непосредственного физического смысла, но может рассматриваться как формальная величина такая, что:
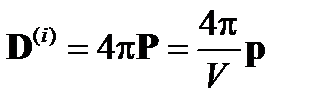
где Р - поляризация; р - полный дипольный момент эллипсоида.
Так как  [1, с. 43],
[1, с. 43], 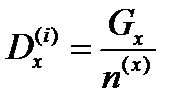 , где
, где  коэффициент деполяризации.
коэффициент деполяризации.
Тогда  .а
.а  . Таким образом, мы имеем:
. Таким образом, мы имеем:
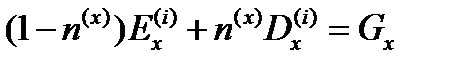
| (35) |
Подставив определение
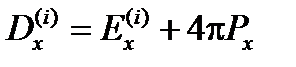
получим:
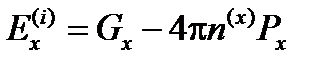 .
.
Член 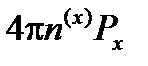 называют деполяризующим полем.
называют деполяризующим полем.
Для напряженности поля внутри эллипсоида, положив
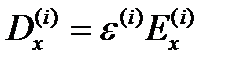 подучим из (35);
подучим из (35);

Полный дипольный момент эллипсоида:
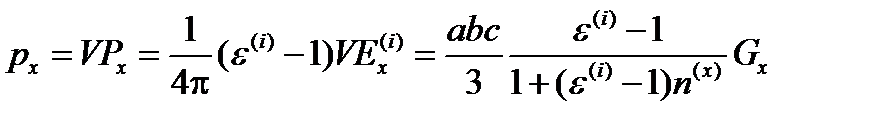
Для произвольной системы координат можно записать:
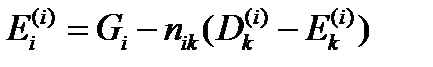
Переход к случаю диэлектрической проницаемости среды, отличной от единицы, производится заменой 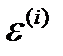 на
на 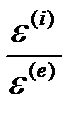 :
: