Неоднородные среды

Использование в науке и технике материалов, обладающих слож­ной структурой, приводит к необходимости решения ряда специфиче­ских задач, порождаемых наличием в среде неоднородностей, под кото­рыми будем понимать отклонения локальных значений материальных характеристик среды от некоторых заданных.

Расчет диэлектрических свойств таких неоднородных сред, как из­вестно, сводится в общем случае к проблеме многих тел и, следователь­но, имеет те же трудности. Несмотря на это, разработаны и используют­ся приближенные методы вычисления эффективной диэлектрической проницаемости и поля таких систем.Диэлектрическая проницаемость £ неоднородных диэлектриков является случайной функцией координат, а это в свою очередь приводит к появлению случайных составляющих напряженности электрического поля Е и индукции D. Причинами отмеченной неоднородности могут быть поликристал­личность, пористость, наличие дефектов и т.д. Область с однородными свойствами будем называть зернами неоднородности.

На рис.8 схематически изображе­ны в случае а - поликристалл, а в слу­чае б - композит. В первом случае зер­но неоднородности - кристаллит, во втором - изотропное эллипсоидальное включение. Ориентация кристаллофи­зических осей кристаллита или глав­ных осей эллипсоида определяет реак­цию зерна неоднородности на внешнее поле [6].В дальнейшем будем для просто­ты рассматривать диэлектрическую смесь, состоящую из двух изотропных компонентов. Между случайной и ре­гулярной составляющими полей суще­ствует связь:

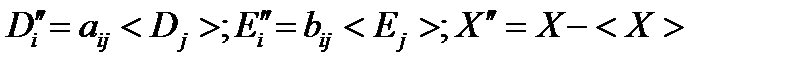
(25)

Величина, стоящая в круглых скобках, устанавливает связь между средними значениями полей < D > и < Е > и представляет собой эффек­тивную диэлектрическую проницаемость. Из формулы (25) видно, что даже у смеси изотропных компонентов эффективная проницаемость является, вообще говоря, тензором. Для вычисления диэлектрических свойств матричных сред ввиду простоты используют сингулярное приближение. (Под матричной сре­дой мы подразумеваем неоднородную среду, через которую можно провести кривую, проходящую через весь диэлектрик и полностью ле­жащую в пределах одного компонента, который называется матрицей). Оно распространяется на широкий класс сред, для которых можно вве­сти понятие эффективного зерна неоднородности (усредненного по раз­мерам зерна в различных направлениях). Последнее имеет смысл в тех случаях, когда распределение по форме зерен изотропно или полностью упорядочено (механическая текстура). Это утверждение верно и для матричных смесей со случайным распределением включений, обла­дающим изотропией.

Если включения другой фазы распределены в матрице регулярным образом, использование сингулярного приближения сопряжено с неко­торыми трудностями и требует модификации метода.

При периодическом распределении включений с тензором диэлек­трической проницаемости в матрице, тензор диэлектрической проницаемости которой 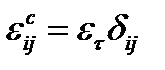, электрическое поле - регулярная функция координат, причем в отсутствие свободных зарядов эта функ­ция обладает периодичностью.

Рассмотрим волновое уравнение в виде

(26)

Для решения задач о неоднородных средах вводят вспомогатель­ное поле, которое отличается от рассматриваемого лишь значениями материальных характеристик:

(27)

Решение задачи (27) для среды сравнения считается известным.

Из (26), (27) получим:

где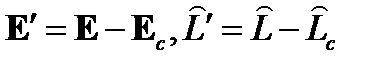

Введя функцию Грина оператора 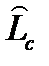, запишем:

(28)

Иногда (28) можно представить в виде ряда

Произведя усреднения

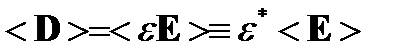
где 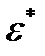- тензор эффективных диэлектрических проницаемостей и

для получим: