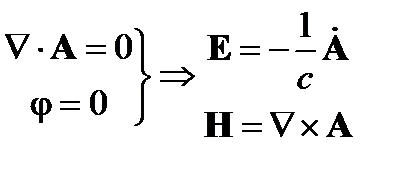Уравнения Максвелла. Потенциалы
Уравнения Максвелла для электромагнитного поля в вакууме:
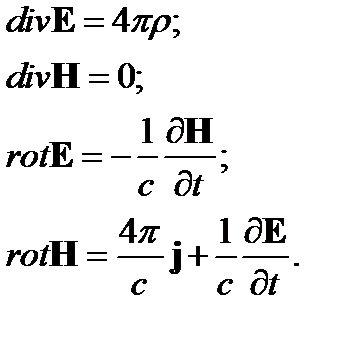
или

| (1) |
Теорема Гаусса в операторной форме:

Теорема Стокса в операторной форме (рис.1):
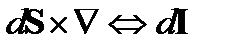
где 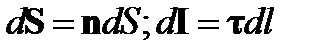
Потенциалы электромагнитного
поля:
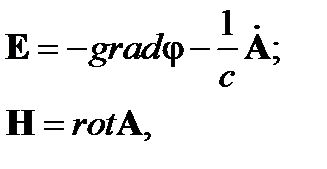
|  (2) (2)
|
где 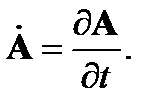
Подставим соотношения (2) в уравнения Максвелла (1):
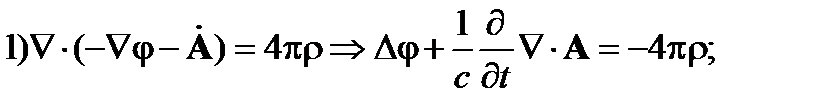
| (3) |
 это уравнение превращается в тождество, так как
это уравнение превращается в тождество, так как 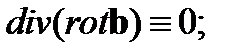
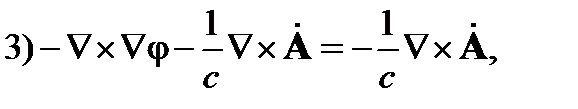 так как
так как 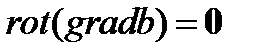 получим тождество
получим тождество 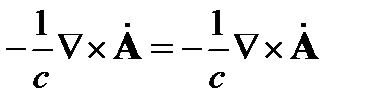
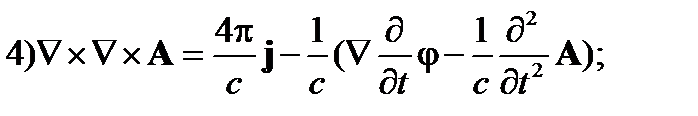
Раскрыв двойное векторное произведение, получим:

| (4) |
Градиентная инвариантность
Если заданы потенциалы А и 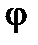 , то этим вполне однозначно задаются Е и Н, а значит, и поле. Однако одному полю могут соответствовать разные потенциалы [2, § 18]:
, то этим вполне однозначно задаются Е и Н, а значит, и поле. Однако одному полю могут соответствовать разные потенциалы [2, § 18]:
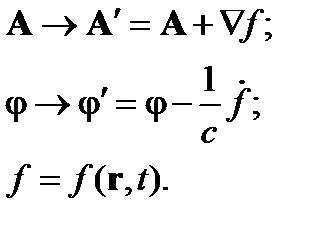
| (5) |
При таком переходе
 и
и 

Таким образом, физический смысл имеют лишь те величины, которые инвариантны по отношению к преобразованию потенциалов (5). Поэтому все уравнения должны быть инвариантны относительно этого преобразования. Эту инвариантность называют градиентной (калибровочной).
Калибровки
Калибровками называются дополнительные ограничения, которые накладываются на потенциалы А и  , чтобы уравнения для потенциалов в конкретном случае были удобны для решения.
, чтобы уравнения для потенциалов в конкретном случае были удобны для решения.
1. Калибровка Лоренца:

| (6) |
С учетом градиентной инвариантности (5) из (6) получим:
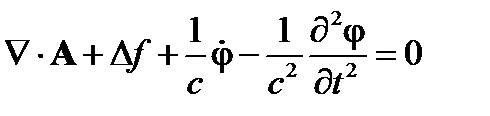
Отсюда следует условие, ограничивающее вид 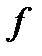 в градиентном преобразовании:
в градиентном преобразовании: 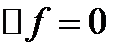 , где □ - оператор Даламбера,
, где □ - оператор Даламбера,
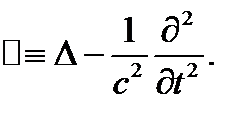
| (7) |
Из уравнения Максвелла  в формуле (3) с учетом уравнения (6) получим:
в формуле (3) с учетом уравнения (6) получим:

| (8) |
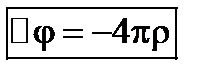
Для 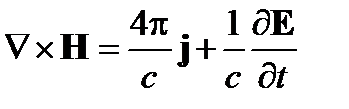 получим:
получим:
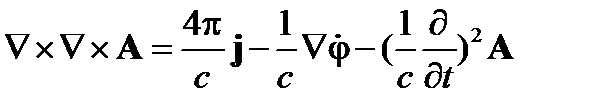
Подставим в (5) 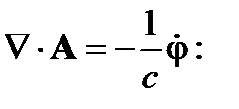
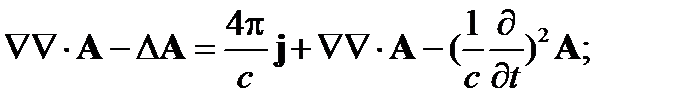
| (9) |
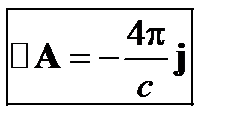
2. Калибровка Кулона:
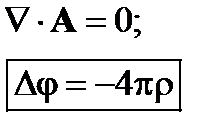
Условие на f:
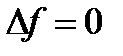
3. Калибровка поперечных волн: