Функция Грина волнового уравнения

 

Для нахождения функции Грина воспользуемся преобразованиями Фурье:

В частности, для фурье-образа дельта-функции получим:

Использование фурье-преобразований позволяет перейти от диф­ференциальных уравнений к алгебраическим по правилам замены опе­раторов алгебраическими множителями:

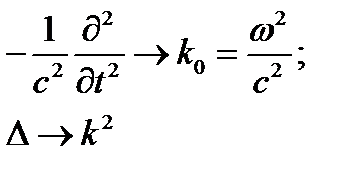
Функция Грина оператора Даламбера:

Перейдем к фурье-образу по времени:

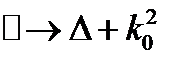- оператор Гельмгольца;

Перейдем к фурье-образу по координатам:

 

 

Связь фурье-образа с прообразом:

 

(10)

 

 

Вычислим интеграл (10). Перейдем к сферическим координатам:

Проинтегрируем по углу:

Данный интеграл находится с помощью теоремы о вычетах [5, с. 212]. Знаменатель имеет два полюса: k=+k₀. Оба они лежат на действительной оси. Выберем контур интегрирования, как пока­зано на рис.З. Вычет подынтегральной функции в точке k₀ (полюс первого порядка) равен

Тогда

 

Здесь воспользовались свойством четности дельта-функции. Перейдя к исходным переменным

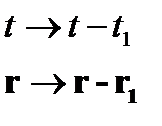
получим:

 

Сделаем замену переменных:

 

где

 

Это дает: