Определение 50. Отображение 
называется тождественным, если 
, и обозначается 
.
Замечание. Пусть 
- функция, тогда 
и 
Доказательство. 
.
Определение 51. Отображение 
называется обратимым, если существует отображение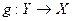 
, такое, что. fg = 
и gf = 
. В этом случае функция g называется обратной для функции f.
Замечание. Если в определении 51 выполняется 1-ое равенство то функция g называется правой обратной функцией для f, а если 2-ое то левой обратной функцией для f.
Лемма 1. Пусть , 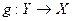- функции. Если gf= 
, то f – инъективная функция, а g – сюръективная функция.
Доказательство. 1) Покажем что f - инъективная функция. Проверим, что выполняется определение 46.
Пусть f (
) = f (
). Покажем, что = . Действительно, 
() 
gf () 
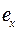g (f ())= g (f ()) gf () 
() 
x -инъективна.
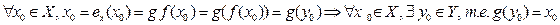
2) Покажем, что g -сюръективная функция.
g - сюръективная функция.
