Определение 14. Бинарным отношением называется всякое множество упорядоченных пар.
В математике при рассмотрении связи между объектами используют термин «отношение». Примерами отношений являются:
1) «
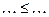» - на множестве ℝ.
2) «
» - на множестве P(U).
3) «
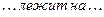» - между множеством всех точек плоскости и множеством всех прямых:
 | |||||
 |  | ||||
M N K
a b c
Упорядоченные пары (M,a),(N,b),(K,c) удовлетворяют условию третьего пункта, а (M,b) не удовлетворяет условию третьего пункта.
Для того, чтобы определить бинарное отношение, достаточно задать множество объектов, для которых имеет смысл говорить о данном отношении, и выбрать из него те пары объектов, которые удовлетворяют рассматриваемому отношению.
Определение 15. Бинарным отношением между множествами A и B называется всякое подмножество множества 
.
Бинарные отношения обозначают следующим образом: 
. Если 
, то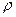 
называется бинарным отношением на множестве A.
Замечание. Если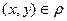 
, где 
, то говорят, что элемент 
находится в отношении 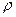с элементом 
, и часто пишут 
, т.е. 
.
Определение 16. Пусть R – бинарное отношение между множествами A и B. Областью определения бинарного отношения R называется множество первых координат всех пар из R, и обозначается Dom R, т.е. 
.
Определение 17. Пусть R – бинарное отношение между множествами A и B. Областью значений бинарного отношения R называется множество вторых координат всех пар из R, и обозначается Im R, т.е. 
.
Определение18. Пусть R – бинарное отношение между множествами A и B. Множество D(R)= Dom R 
Im R называется областью отношений бинарного отношения R.
Определение 19. Пусть 
- множества, n-арным отношением между множествами называется всякое подмножество множества 
.
При n=1 мы получаем унарные отношения, при n=2 - бинарные отношения, при n=3 – тернарные отношения.
