Определение 20. Бинарное отношение R на множестве А называется рефлексивным, если ∀ a  А: (а;a)
А: (а;a)  R (т.е. aRa).
R (т.е. aRa).
Пример. «=»на множестве ℝ.
Определение 21. Бинарное отношение R на множестве А называется антирефлексивным, если ∀ а  А: (a;a)
А: (a;a) 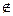 R.
R.
Пример. «<»на множестве ℝ.
Определение 22. Бинарное отношение R на множестве А называется симметричным, если  a,b
a,b  A, из (а,b)
A, из (а,b)  R
R  (b,a)
(b,a)  R.
R.
Пример. «∥» на множестве всех прямых в пространстве, «=» на множестве ℝ.
Определение 23. Бинарное отношение R на множестве А называется антисимметричным, если  a,b
a,b  A, из (а,b)
A, из (а,b)  R и (b,a)
R и (b,a)  R
R  a=b.
a=b.
Пример. Отношения 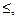
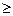 ,=,<,> на множестве ℝ.
,=,<,> на множестве ℝ.
Определение 24. Бинарное отношение R на множестве А называется транзитивным, если  a,b,с
a,b,с  A, из (а,b)
A, из (а,b)  R и (b,с)
R и (b,с)  R
R  (а,с)
(а,с)  R.
R.
Пример. «∥» на множестве всех прямых в пространстве, отношения 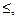
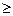 ,=,<,> на множестве ℝ
,=,<,> на множестве ℝ
Cвойства отношений
Пусть 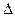 =
= 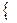 (a,a)|a
(a,a)|a  A
A 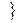 - диагональ декартова квадрата A2=A
- диагональ декартова квадрата A2=A  A.
A.
Лемма 1. Пусть R - бинарное отношение на множестве A. Тогда
1) R рефлексивно 
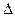
 R;
R;
2) R антирефлексивно  R
R 
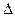 =
=  .
.
Доказательство.
1) а) Необходимость. Пусть R рефлексивно. Покажем, что 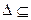 R. Действительно,
R. Действительно, 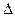 =
= 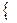 (а,а) |а
(а,а) |а  А
А 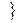
 R по определению 20, т.к. ∀ a
R по определению 20, т.к. ∀ a  А: (а;a)
А: (а;a)  R
R 
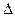
 R.
R.
б) Достаточность. Пусть 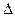
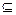 R. Покажем, что R рефлексивно. Пусть а
R. Покажем, что R рефлексивно. Пусть а  А. Покажем, что (а,а)
А. Покажем, что (а,а)  R. Так как (а,а)
R. Так как (а,а) 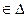
 R, т.е. (а,а)
R, т.е. (а,а)  R
R  по определению 20 R рефлексивно.
по определению 20 R рефлексивно.
2) а) Необходимость. Пусть R антирефлексивно. Покажем, что R 
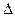 =
=  . Допустим, что R
. Допустим, что R 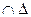


 (x,y)
(x,y)  R
R 
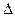
 (x,y)
(x,y)  R и (x,y)
R и (x,y) 
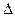
 x=y, т.е. (x,x)
x=y, т.е. (x,x)  R –противоречие с определением 21
R –противоречие с определением 21  допущение неверно
допущение неверно  R
R 
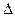 =
=  .
.
б) Достаточность. Пусть R 
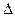 =
=  . Покажем, что R антирефлексивно. Для этого достаточно показать, что R удовлетворяет определению 21. Пусть а
. Покажем, что R антирефлексивно. Для этого достаточно показать, что R удовлетворяет определению 21. Пусть а  А. Покажем, что (а,а)
А. Покажем, что (а,а) 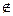 R. От противного, допустим, что (а,а)
R. От противного, допустим, что (а,а)  R
R  (a,a)
(a,a)  R
R 
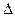 =
=  , противоречие
, противоречие  (а,а)
(а,а) 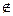 R.
R.  Лемма доказана.
Лемма доказана.
Определение 25. Пусть R – бинарное отношение между множествами A и B.
Множество R-1 = 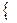 (m,n) | (n,m)
(m,n) | (n,m)  R
R  называется бинарным отношением, обратным бинарному отношению R.
называется бинарным отношением, обратным бинарному отношению R.
Лемма 2. Пусть R - бинарное отношение на множестве A. Тогда
1) R симметрично  R-1=R;
R-1=R;
2) R антисимметрично  R
R  R-1
R-1 
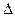 .
.
Доказательство. 1) а) Необходимость. Пусть R симметрично. Методом встречных включений покажем, что R-1=R.
Докажем, что R-1  R. Действительно, R-1 =
R. Действительно, R-1 = 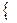 (m,n) | (n,m)
(m,n) | (n,m)  R
R  . Но так как R симметрично, то, по определению 22, из (n,m)
. Но так как R симметрично, то, по определению 22, из (n,m)  R следует (m,n)
R следует (m,n)  R
R 
R-1  R.
R.
Доказательство R  R-1 проводится аналогично.
R-1 проводится аналогично.
б) Достаточность. Пусть R-1=R. Покажем, что R симметрично. Пусть (n,m)  R. Покажем, что (m,n)
R. Покажем, что (m,n)  R. Так как (n,m)
R. Так как (n,m)  R= R-1
R= R-1  (n,m)
(n,m)  R-1
R-1  (m,n)
(m,n)  R
R  R симметрично.
R симметрично.
2) а) Необходимость. Пусть R антисимметрично. Покажем, что R  R-1
R-1 
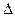 . Пусть (x,y)
. Пусть (x,y)  R
R  R -1
R -1  (x,y)
(x,y)  R -1 и (x,y)
R -1 и (x,y)  R
R  (x,y)
(x,y)  R и (y,x)
R и (y,x)  R, и так как R антисимметрично
R, и так как R антисимметрично  x=y.
x=y.
б) Достаточность. Пусть R - бинарное отношение на А и R  R-1
R-1 
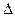 . Докажем, что R антисимметрично. Предположим, что это не так. Тогда найдётся хотя бы одна пара (a,b)
. Докажем, что R антисимметрично. Предположим, что это не так. Тогда найдётся хотя бы одна пара (a,b)  R такая, что (b,a)
R такая, что (b,a)  R и a ≠ b
R и a ≠ b  (по определению R-1)
(по определению R-1)  (a,b)
(a,b)  R и (a,b)
R и (a,b)  R-1. Таким образом, (a,b)
R-1. Таким образом, (a,b)  R
R  R-1
R-1 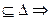 a=b, противоречие
a=b, противоречие  предположение неверно. Лемма доказана.
предположение неверно. Лемма доказана.
Определение 26. Пусть R, S - бинарные отношения на множестве А.
Множество R.S={(x,y) |  y
y  A: (x,y)
A: (x,y)  S и (y,z)
S и (y,z)  R} называется произведением бинарных отношений R и S.
R} называется произведением бинарных отношений R и S.
Лемма 3. Пусть R - бинарное отношение на множестве A. Тогда R транзитивно  R.R
R.R  R.
R.






