Теорема 1. Для операций над множествами справедливы следующие свойства:
| 1. А È B=В È А | 1’. А Ç B=В Ç А | Коммутативность |
| 2. (А È B) È С= А È (B È С) | 2’. (А Ç B) Ç С= А Ç (B Ç С) | Ассоциативность |
| 3. А È (B Ç С)=(А È В) Ç (А È С) | 3’. А Ç (В È С)=(А È В) Ç (А È С) | Дистрибутивность |
| 4. А È А=А | 4’. А Ç А=А | Идемпотентность |
5. 
| 5’. 
| Законы де Моргана |
| 6. А È (А Ç В)=А | 6’. А Ç (А È В)=А | Законы поглощения |
7. А È  = U
8. А È U= U
9. А È Æ= А = U
8. А È U= U
9. А È Æ= А
| 7’. А Ç  =Æ
8’. А Ç U=A
9’. А Ç Æ=Æ =Æ
8’. А Ç U=A
9’. А Ç Æ=Æ
| Законы пустого и универсального множества |
10.  =А =А
| Закон инволюции | |
11. А\В=А Ç 
| Закон исключения разности |
Доказательство. Докажем свойство 1.
Левая часть выражения 1  состоит по определению 5 из элементов, принадлежащих либо А, либо В, либо А и В. Правая часть
состоит по определению 5 из элементов, принадлежащих либо А, либо В, либо А и В. Правая часть  состоит из элементов, принадлежащих либо В, либо А, либо В и А. Очевидно, что левая и правая часть равенства 1 состоит из одних и тех же элементов следовательно по определению 1,
состоит из элементов, принадлежащих либо В, либо А, либо В и А. Очевидно, что левая и правая часть равенства 1 состоит из одних и тех же элементов следовательно по определению 1,  .
.
Докажем свойство 11: 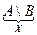 =
=  методом встречных включений
методом встречных включений
а)  и
и  и
и 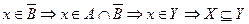
б)  и
и  и
и 
в) из 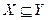 и
и 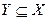 следует
следует 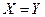
Остальные свойства доказываются аналогично.
Замечание 1. Операции пересечения и объединения можно сформулировать в общем виде для конечного и бесконечного числа множеств.
Замечание 2. Множество называется конечным, если оно состоит из конечного числа элементов. В бесконечном случае различают счетные множества (например, ℤ) и множества мощности континуум (например, ℝ).
Если конечное множество M состоит из n элементов, то пишут | M |= n, т.е. | M | -мощность множества M.
Таким образом, мощность конечного множества – это число элементов данного множества.
Пусть M – множество. Обозначим через P(M) - совокупность всех подмножеств множества M.
Утверждение. Если | M |= n, то | P(M) |= 2n. Другими словами, у конечного множества мощности n существует ровно 2n попарно различных подмножеств.
Например, если А={1,2}, то | A |=2 и | P(A) |=4.






