Определение 29. Бинарное отношение R на множестве А называется отношением порядка, если оно антисимметрично и транзитивно.
Пример. £, ³, <, >, = на множестве ℝ
Определение 30. Бинарное отношение R на множестве А называется отношением предпорядка, если оно рефлексивно и транзитивно.
Пример. £, ³, = на множестве ℝ.
Определение 31. Отношение порядка R на множестве А называется отношением строгого порядка, если оно антирефлексивно.
Пример. <, >.
Определение 32. Отношение порядка R на множестве А называется отношением нестрогого порядка, если оно рефлексивно.
Пример. £, ³, = на множестве ℝ.
Замечание. Из свойств антирефлексивности и транзитивности следует свойство антисимметричности.
По этому определение 31 ⇔ определению 31’.
Определение 31’. Отношение порядка R на множестве А называется отношением строгого порядка, если оно антирефлексивно и транзитивно.
Пример. 1) Отношение кратности «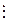
» на множестве ℕ рефлексивно, т.к. a 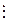a, и транзитивно, т.к. из а 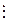b и b 
с Þ a с. Значит оно является отношением предпорядка на ℕ.
2) Отношение «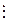» на ℤ не антисимметрично(из а b и b а Þ а= ∓ b), рефлексивно, транзитивно Þ Z – отношение предпорядка и не является отношением порядка.
Определение 33. Бинарное отношение R на множестве А называется связанным (связным), если " а, b Î А, а 
b выполняется одно и только одно из условий: либо (а,b) Î R, либо (b,а) Î R.
Пример. 1) < на ℕ – связное
2) ⊆ на P (U): существуют множества, такие, что A B, но А⊈В и В⊈А.Значит R не является связным на P (U).
Определение 34. Отношение порядка на множестве А называется отношением линейного порядка, если оно связано. В противном случае отношение порядка называется отношением частичного порядка.
Определение 35. Непустое множество А с заданным на нем отношением порядка R называется упорядоченным множеством и обозначается (А, R).
Пример. (ℕ, £) – упорядоченное множество.
Определение 36. Упорядоченное множество (А, R) называется линейно-упорядоченным, если R -отношение линейного порядка. Если R - отношение частичного порядка, то упорядоченное множество (А, R) называется частично-упорядоченным.
Определение 37. Пусть (А, R)- упорядоченное множество. Элемент а Î А называется минимальным (максимальным) элементом множества А, если " x Î А: из (х, а)Î R Þ x=a (из (а,х)Î R Þ x=a).
Во множестве может быть несколько минимальных и максимальных элементов.
Пример. А ={2,3,4,6,8,12,24}-множество всех натуральных делителей числа 24, отличных от 1. На А рассмотрим отношение «|» - делит без остатка.
Покажем, что 2-минимальный элемент:
Из x ÎA и х |2 Þ х= 2
Покажем, что 3-минимальный элемент:
Из x ÎA и х |3 Þ х= 3.
Определение 38. Пусть (А, R) - упорядоченное множество. Элемент аÎ А называется наименьшим (наибольшим) элементом, если " x Î А: (а,х)Î R ((х,а)Î R)
Если во множестве есть наименьший элемент, то он единственен.
Определение 38. Линейное упорядоченное множество называется вполне упорядоченным, если любое его не пустое подмножество содержит наименьший элемент.
Пример. (ℕ, £) - вполне упорядоченное множество.
