Понятие множества является первичным, исходным и не определяется через
другие более простые понятия. Под множеством понимают совокупность объектов, рассматриваемых как единое целое.
Например: множество книг, составляющих данную библиотеку; множество философских учений.
Объекты из которых состоит множество, называются его элементами. Множества обозначают большими буквами латинского алфавита, а его элементы - малыми. Для того, чтобы показать, что какой-либо объект является элементом того или иного множества, вводится понятие принадлежности.
Î - знак принадлежности;
а Î А – читается «а принадлежит множеству А»;
а Ï А – читается «а не принадлежит множеству А».
Для наиболее важных числовых множеств используют фиксированные обозначения:
ℕ - множество всех натуральных чисел;
ℤ - множество всех целых чисел;
ℚ - множество всех рациональных чисел;
ℝ - множество всех действительных чисел.
Множество считается заданным, если по любому объекту можно судить, является ли он элементом данного множества или нет.
Основные способы задания множества:
1. С помощью перечисления элементов.
Если множество А состоит из элементов а1,а2,…,аn, то записывают:
А ={ а1,а2,…,аn }.
Например, М = {-1, 3, y }, ℕ = {1, 2, 3, …}- множество всех натуральных чисел
2. Указание характеристического свойства элементов.
А ={x|…} (читается «множество А состоит из элементов х таких, что …).
Например, множество всех рациональных чисел ℚ = 
m Î ℤ, n Î ℕ }
Определение 1. Множества А и В называют равными, если каждый элемент множества А принадлежит множеству В и каждый элемент множества В принадлежит множеству А то есть: 
: 
и 
: 
. И обозначается А = В.
Другими словами, множества равны, если они состоят из одних и тех же элементов. Например, А ={1,2,3}, В ={1,2,1,3}. Тогда А=В.
Если множества А и В не равны, то записывают А¹В.
Определение 2. Если каждый элемент множества А принадлежит множеству В, то множество А называется подмножеством множества В и обозначается А Í В.
Иными словами, А 
В, если : .
Í - знак включения.
АÍВ – читается «А содержится в В», «А включается в В».
Определение 3. Если А Í В и А¹В, то множество А называется собственным подмножеством множества В и обозначается А Ì В.
Для доказательства равенства множеств А и В, согласно определению 1 и определению 2, используют метод встречных включений, который заключается в том, что из А В и В А следует, что А=В.
Определение 4. Множество, не содержащее ни одного элемента, называется пустым и обозначается Æ.
Пустое множество единственно. Пустое множество является подмножеством любого множества.
Операции над множествами.
Над множествами вводятся три основные операции:
- пересечение - Ç;
- объединение - È;
- разность - \.
Определение 5. Пересечением множеств А и В называется множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В одновременно и обозначается АÇВ, т.е. АÇВ={x| xÎА и xÎВ}.
Операции над множествами удобно пояснять на диаграммах Эйлера-Венна.
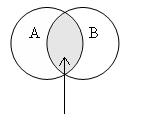xÎ АÇВ<=> xÎА и xÎВ
xÏ АÇВ<=> xÏА или xÏB
АÇВ
Определение 6. Объединением множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В, и обозначается: АÈВ, т.е. АÈВ={x| xÎА или xÎВ}.
xÎ АÈВ<=> xÎА или xÎВ
xÏ АÈВ<=> xÏА и xÏB
Замечание. Если элемент х принадлежит множеству А, то он принадлежит объединению множества А с любым другим множеством.
Определение 7. Разностью множеств А и В называется множество, состоящее из всех элементов, принадлежащих множеству А и не принадлежащих множеству В, и обозначается: А\В, т.е. А\В={x| xÎА и xÏВ}.
А\В
Определение 8. Если А Í В, то разность В\A называется дополнением к множеству А во множестве В.
Определение 9. Универсальным множеством называется множество, содержащие все рассматриваемые нами множества (в процессе какого-либо рассуждения) в качестве своих подмножеств и обозначается U.
На диаграмме Эйлера- Венна универсальное множество обычно изображают прямоугольником.
 |
Определение 10. Дополнением множества А называется разность U\A и обозначается 
.
