Определение 39. Бинарное отношение f между множествами A и B называется функциональным отношением, если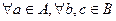 
из (a, b) 
f и (a, c) f 
b = c.
A
B A B
функциональное отношение, не является функцион. отношением
но не функция
Определение 40. Функциональное отношение f между множествами A и B называется функцией или отображением A в B, если Dom f = A,и обозначается
f: A 
B или A B.
A f
Функция и
функциональное отношение
B
Замечание. Если f: A B – функция, то каждому элементу a A соответствует единственный элемент b B и записывается f (a)= b 
(a, b) f a f b.
Определение 41. Пусть f: A B функция, a A, b B. Если f (a)= b, то b называется образом элемента a при отображении f; элемент a называется прообразом элемента b при отображении f.
A
f
B
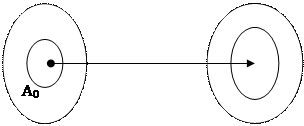
Определение 42. Пусть дана функция f: A B, A 0 
A. Множество f (A 0)={ f (a)| a A 0} называется образом множества A 0 при отображении f.
 |
A B
f
 |
f (A 0)
Определение 43. Пусть f: A B функция, b B.
Множество f -1(b)={ a A | f (a)= b } называется полным прообразом элемента b при отображении f.
 |  |
A
B
 |
a1, a2 – прообразы b.
{ a 1, a 2} – полный прообраз при отображении f.
Определение 44. Пусть f: A B функция, B 0 B.
Множество f -1(B 0)=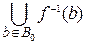 
называется полным прообразом множества B 0 при отображении f.
Отметим, что f -1(B)= A, f (A) B.
Определение 45. Отображение f: X Y называется инъективным (или взаимно-однозначным отображением X в Y), если 
x 1, x 2 X из x 1 
x 2 f (x 1) f (x 2). «разным соответствуют разные»
Замечание. На практике при проверке свойства инъективности используют другую формулировку.
Определение 46. Отображение f: X Y называется инъективным, если x 1, x 2 X из f(x 1)= f (x 2) x 1= x 2. «если образы равны, то и прообразы равны»
Определение 47. Отображение f: X Y называется сюръективным (или отображением X на Y), если Im f совпадает с Y (Im f = Y), т. е.
y Y 
x X т. что f (x) = y. «для всякого образа найдётся прообраз»
Определение 48. Отображение f: X Y называется биективным (взаимно-однозначным отображением X на Y), если f инъективно и сюръективно.
Биективное отображение называется биекцией, инъективное – инъекцией, сюръективное – сюръекцией.
 |  |
A f B
не является инъекцией
 |
f B
A инъекция, не сюръекция
 | |
 |
A B
f
сюръекция, инъекция
биекция
 |
