Степенная функция  с натуральным показателем непрерывна на R как произведение n непрерывных функций
с натуральным показателем непрерывна на R как произведение n непрерывных функций  . Если
. Если 
 , то степенная функция строго возрастает и поэтому обратима на всем множестве R (см. рис. 1.19):
, то степенная функция строго возрастает и поэтому обратима на всем множестве R (см. рис. 1.19):
Если 
 , то степенная функция с четным показателем
, то степенная функция с четным показателем 
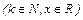 не обратима на всем множестве R (так как разным значениям х 0 и - х 0 соответствует одно значение функции: (х 0)2k=(- х 0)2k= y 0).
не обратима на всем множестве R (так как разным значениям х 0 и - х 0 соответствует одно значение функции: (х 0)2k=(- х 0)2k= y 0).
Если рассмотреть функцию на положительной части области определения 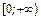 , то для нее существует обратная функция
, то для нее существует обратная функция 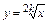 , которая также является строго возрастающей
, которая также является строго возрастающей
Рассмотрим степенную функцию с целым отрицательным показателем 
 . Она определена и непрерывна при
. Она определена и непрерывна при  и по определению степени с целым показателем записывается в виде
и по определению степени с целым показателем записывается в виде 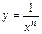
Дадим определение степенной функции  с рациональным показателем
с рациональным показателем  :
:
Если 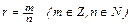 , то положим
, то положим  .
.
Функция 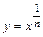 непрерывна и строго возрастает при x>0. Функция
непрерывна и строго возрастает при x>0. Функция  непрерывна при t>0 и строго возрастает, если m>0; строго убывает при m<0.
непрерывна при t>0 и строго возрастает, если m>0; строго убывает при m<0.
Поэтому, согласно теореме о непрерывности сложной функции, степенная функция хr непрерывна на (0;+¥) и возрастает при r >0, а убывает при r <0.
Лемма 1. Для функций  имеет место
имеет место  .
.
Пусть теперь x - произвольная точка числовой прямой и 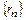 - последовательность рациональных чисел, сходящаяся к х:
- последовательность рациональных чисел, сходящаяся к х:  . Предполагая a >0, положим по определению:
. Предполагая a >0, положим по определению: 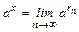 .
.
Функция ах (а >0), определенная для  равенством
равенством 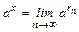 называется показательной с основанием a.
называется показательной с основанием a.
Свойства функции  :
:
1. При a >1 функция строго возрастает, при 0< a <1 – строго убывает на всей числовой оси.
2.  .
.
3. 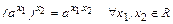 .
.
4. Функция  непрерывная на R.
непрерывная на R.
5. при  .
.
6. множество значений функции при 0< a ¹1- 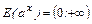 .
.
Используя теорему о существовании и непрерывности обратной функции, на промежутке 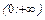 определим функцию, обратную к показательной
определим функцию, обратную к показательной 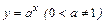 . Эта функция называется логарифмической и обозначается
. Эта функция называется логарифмической и обозначается  .
.
Показательная функция у= ах при  возрастает, поэтому обратная функция
возрастает, поэтому обратная функция  при a >1 также строго возрастает и непрерывна:
при a >1 также строго возрастает и непрерывна: 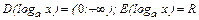 . При 0< a <1 функция
. При 0< a <1 функция  также непрерывна и строго убывает:
также непрерывна и строго убывает:
Пусть 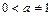 , то по свойствам взаимно-обратных функций справедливы равенства:
, то по свойствам взаимно-обратных функций справедливы равенства: 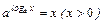 ,
,  .
.
Если 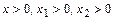 , то из свойства 2 показательной функции и формулы (4) следует, что:
, то из свойства 2 показательной функции и формулы (4) следует, что:
1)  ; 2)
; 2) 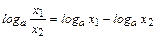 ; 3)
; 3)  .
.
4)  или при x=b
или при x=b  .
.
Степенная функция с вещественным показателем
Полагают, что: 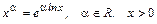 .
.
Функция  - непрерывна при x>0 как сложная функция двух непрерывных:
- непрерывна при x>0 как сложная функция двух непрерывных:  и
и  .
.
Из равенства (1) и свойств показательной, логарифмической функций следует: при 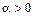 функция
функция  строго возрастает, а
строго возрастает, а  строго убывает на
строго убывает на 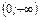 .
.
Функцию  , где u(x), v(x) определены на D Í R и
, где u(x), v(x) определены на D Í R и 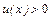 называют показательно-степенной и обозначают
называют показательно-степенной и обозначают
 .
.
Если u и v - непрерывны на D, то uv - непрерывна как сложная функция.






