Лемма 1. Если 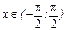 и
и 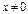 , то
, то
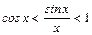 . (1)
. (1)
 gРассмотрим единичный круг с центром в начале координат. Пусть
gРассмотрим единичный круг с центром в начале координат. Пусть 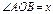 ,
, 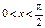 , тогда ВС= sinx, ОС= cosx, ОА=1. Из подобия DОВС
, тогда ВС= sinx, ОС= cosx, ОА=1. Из подобия DОВС  DОДА имеем
DОДА имеем 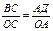 , поэтому AД=tgx.
, поэтому AД=tgx.
Для 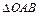 :
: 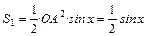 .
.
Для сектора АОВ: 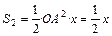 .
.
Для 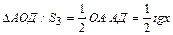 .
.
Из неравенств 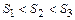 следует
следует
 . (2)
. (2)
Если  , то
, то  и из (2) имеем
и из (2) имеем 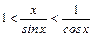 . Из свойств обратных величин получаем неравенство (1).
. Из свойств обратных величин получаем неравенство (1).
функции 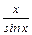 и
и 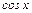 - четные, поэтому неравенство (1) справедливо и при х Î
- четные, поэтому неравенство (1) справедливо и при х Î 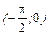 .n
.n
Лемма 2.  справедливо неравенство
справедливо неравенство 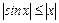 .
.
Теорема. Функции  ,
, 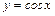 непрерывны на R.
непрерывны на R.
gПусть  - произвольная точка множества R. Тогда
- произвольная точка множества R. Тогда  .
.
из неравенства (4) имеем:  , а в силу ограниченности функции
, а в силу ограниченности функции 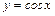 :
: 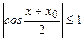 . Поэтому
. Поэтому  .
.
При 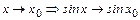 , а функция
, а функция  непрерывна в точке
непрерывна в точке  .
.
для доказательства непрерывности функции  в точке
в точке  оценим разность
оценим разность 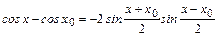 :
: 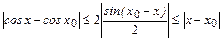 .n
.n
Лемма 3 (Первый замечательный предел).
Если 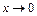 , то
, то  , т.е.:
, т.е.:
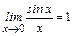 . (5)
. (5)
gв неравенстве (1) перейдем к пределу при 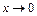 . по теореме о пределе промежуточной функции, учитывая непрерывность
. по теореме о пределе промежуточной функции, учитывая непрерывность 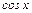 (
( ), имеем (5).n
), имеем (5).n
Обратные тригонометрические функции
Рассмотрим функцию  для
для 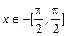 (см. рис. 1.18). Она непрерывна, строго возрастает и принимает значения из [-1,1]. По теореме о существовании обратной функции на отрезке [–1,1] определена функция, обратная к функции
(см. рис. 1.18). Она непрерывна, строго возрастает и принимает значения из [-1,1]. По теореме о существовании обратной функции на отрезке [–1,1] определена функция, обратная к функции  , которая непрерывна и строго возрастающая. Ее обозначают
, которая непрерывна и строго возрастающая. Ее обозначают  ,
, 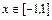 . График функции
. График функции  симметричен графику синусоиды, заданной на
симметричен графику синусоиды, заданной на 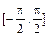 относительно прямой y=x.
относительно прямой y=x.
Рассмотрим функцию  (
(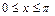 ), которая непрерывна и строго убывает (см. рис 1.18). по теореме об обратной функции на отрезке [–1,1] определяется
), которая непрерывна и строго убывает (см. рис 1.18). по теореме об обратной функции на отрезке [–1,1] определяется  , которая также непрерывна и строго убывает.
, которая также непрерывна и строго убывает.
Функция 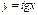 (
(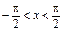 ) непрерывна, строго возрастает, принимая значения из (–¥;+¥) (см. рис. 1.18). Обратная к ней функция, которую обозначают
) непрерывна, строго возрастает, принимая значения из (–¥;+¥) (см. рис. 1.18). Обратная к ней функция, которую обозначают  (х ÎR), - непрерывна и строго возрастает: D(arctg)= (–¥;+¥); E(arctg)=(-p/2; p/2). Поскольку
(х ÎR), - непрерывна и строго возрастает: D(arctg)= (–¥;+¥); E(arctg)=(-p/2; p/2). Поскольку 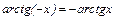 , то функция
, то функция  – нечетная.
– нечетная.
Функцию, обратную к функции 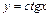 (
(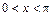 ), обозначают
), обозначают 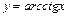 : D(arcсtg)= (–¥;+¥); E(arctg)=(0; p). Она непрерывная и строго убывающая на R.
: D(arcсtg)= (–¥;+¥); E(arctg)=(0; p). Она непрерывная и строго убывающая на R.
1.19. Второй замечательный предел
Теорема. Функция 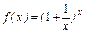 имеет предел при
имеет предел при  :
: 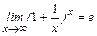 . (1)
. (1)
gФункция  определена при
определена при 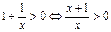 , т.е.
, т.е. 
В параграфе 1.8 доказано, что последовательность 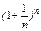 имеет предел:
имеет предел: 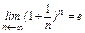 . Покажем, что существует предел функции
. Покажем, что существует предел функции  при
при 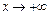 (т.е. рассмотрим функцию на правой части
(т.е. рассмотрим функцию на правой части 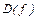 ). Если
). Если 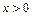 , то
, то  . (2)
. (2)
Не ограничивая общности, можно считать x>1 (нас интересует поведение  при
при 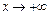 ). Пусть
). Пусть 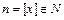 . Из неравенства (2) для обратных величин имеем:
. Из неравенства (2) для обратных величин имеем: 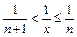 , откуда после прибавления 1 к обеим частям получим:
, откуда после прибавления 1 к обеим частям получим:  . (3)
. (3)
Возведем каждое выражение в неравенстве (3) последовательно в степени (2): 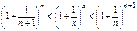 .
.
Пределы крайних величин равны:
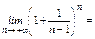
 ;
;
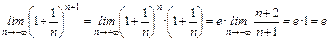 .
.
По теореме о пределе промежуточной функции получим: 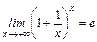 . (4)
. (4)
Рассмотрим левую часть 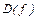 :
: 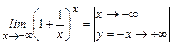 =
=  =
= 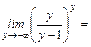
 =
= 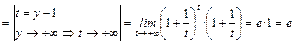 .
.






