Теорема 1. 
.
gФункция 
определена в некоторой окрестности точки x =0 и 
. Сложная функция 
непрерывна в точке x =0 как композиция непрерывных функций: 
. Учитывая, что = 
, имеем: 
.n
Теорема 2. 
; 
.
g 
(если 
, то 
): 
.n
Теорема 3. 
(
).
Докажем при a=1/2, т.е. 
: 
.
Раскрытие неопределенностей
üЕсли 
- б.м.ф. при 
, то 
называют раскрытием неопределенности 
. При этом в дроби 
следует выделить множитель 
в числителе и знаменателе.
üЕсли 
, то частное 
представляет при 
неопределенность 
. Когда f, g - многочлены, то разделив числитель и знаменатель на наибольшую степень, удается применить известные теоремы об арифметических операциях с пределами.
üЕсли f, g - б.б.ф. одного знака, то выражение 
при представляет неопределенность 
.
üЕсли 
, то в произведении 
имеем неопределенность 0×¥
Метод замены переменного при вычислении предела основан на теореме о пределе сложной функции: если существуют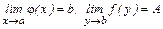 
, причем, 
, то в точке а существует предел сложной функции 
и справедливо равенство 
.
