Пусть a(х), b(х) - б.м.ф. при 
. Хотя 
, все же характер приближения к 0 у них может быть различен.
Две б.б.ф. сравниваются по быстроте стремления к нулю через поведение их отношения 
при 
, где 
в окрестности а:
если 
=0, то 
есть б.м.ф. более высокого порядка;
если = 
, то a(х), b(х) - одного порядка малости;
если =1, то a(х)~b(х) эквивалентные б.м.ф. при ;
если =¥, то b(х) есть б.м.ф. более высокого порядка;
если не существует, то a(х), b(х) не сравнимы.
Бесконечно малые функции a(x), b(x) называются эквивалентными при (пишут a(x)~b(x)), если =1.
Эквивалентными при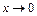 
являются функции:
~ x, 
~ x,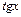 
~ x, 
~ x, 
~ 
, 
~ 
, 
~a x, 
~ x, 
~ x.
При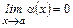 
соотношения остаются в силе и при (при этом следует заменить х на a(х)): ln x =ln(1+(x –1)~(x -1) при x ®1.
Теорема 1 (о замене функций эквивалентными при вычислении пределов). Если при 
имеем две эквивалентные б.м.ф. a~a1, b~b1 и существует 
, то также существует предел отношения 
при и 
. (1)
Теорема 2 (признак эквивалентности б.м.ф). две б.м.ф. эквивалентны a(х)~b(x) при , тогда и только тогда, когда разность a(х)-b(х) при является б.м.ф. более высокого порядка, чем a(х) и b(х).
