Пусть задана числовая функция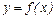 
(
): 
.
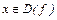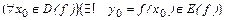Обратная задача: по заданному значению функции у 0 найти соответствующее значение аргумента – решить относительно x уравнение: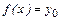 
, 
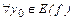. (1)
Если функция f (x) такова, что каждое значение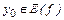 
, она принимает только при одном значении 
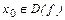, то ее называют обратимой: (
)(
.
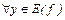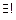
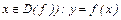Для обратимой функции прямая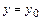 
(
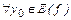) пересечет 
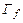в единственной точке 
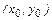, где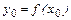 
. Таким образом можно построить функцию x=g(y), обратную данной. Если перейти к прежним обозначениям (x - аргумент), то функция y =g(x) обратная к данной. Взаимно-обратные функции обладают свойствами:
1) 
, 
;
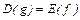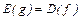2) 
;
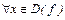
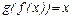3) 
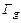симметричен 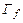относительно прямой y=x.
Теорема. Если функция у = f (x) непрерывна и строго возрастает (строго убывает) на [ а;b ], то на [ А;В ], где А= f (a), В= f (b) определена непрерывная строго возрастающая (строго убывающая) обратная функция x=g(y).
gПусть f(x) - строго возрастает: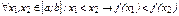 
.
Множество значений непрерывной на отрезке [ a,b ] функции есть отрезок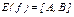 
, поскольку 
.
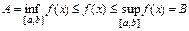Из строгой монотонности имеем, что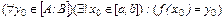 
. Если бы уравнение 
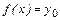имело еще один корень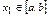 
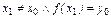(к примеру, 
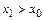), то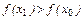 
. Это противоречит условию: 
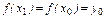. Следовательно, для f на [ a,b ] существует обратная функция x=g(y), для которой D(g) =[A;B], E(g) =[ a;b ].
Покажем, что g строго возрастает на [A;B]:
: 
< 
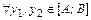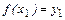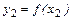Þ х1 < х2. (2)
если бы было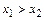 
, то, в силу строгой монотонности функции f, 
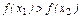. При х1 = х2 имели бы 
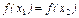. Поэтому справедливо неравенство 
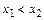, что доказывает монотонность обратной функции.
Докажем непрерывность обратной функции в любой точке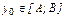 
. Известно, что этому значению соответствует единственная точка 
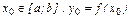или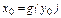 
. Пусть 
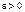(достаточно малое), чтобы 
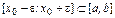и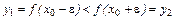 
. Тогда из строгой монотонности следует, что 
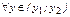соответствующее значение 
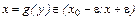. Значит, 
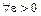можно подобрать окрестность 
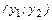точки y0, такую, что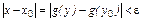 
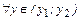. Это подтверждает непрерывность обратной функции в точке y0.
Для концевой точки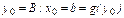 
считаем: 
, 
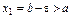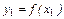. Поэтому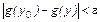 
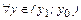.n
