Пусть задано множество М числовых отрезков Dn=[ an;bn ] (nÎN).
Если для отрезков Dn множества М выполнено включение D1ÉD2É … É DnÉ…, т.е. каждый следующий отрезок содержится в предыдущем, то их называют системой вложенных отрезков.
Система вложенных отрезков М будет последовательностью стягивающихся отрезков, если при любом, сколь угодно малом e>0, множество М содержит отрезок с длиной меньше e.
То, что при больших n предел длины n -го отрезка стремится к 0, записывают так: 
(bn-an)=0.
Теорема (О вложенных отрезках). Для последовательности стягивающихся отрезков существует единственная точка, принадлежащая всем отрезкам системы.
gУстановим существование общей точки. Для системы М вложенных отрезков следует, что ("nÎN) ("mÎN) ® a n£bm. (1)
Для двух непустых множеств А={ a n | nÎN}, B={bm | mÎN} выполняется условие (1), значит, по свойству непрерывности множества действительных чисел, существует точка с, принадлежащая всем отрезкам стягивающейся системы, т.е.:
($ c ÎR): ("nÎN)®an£ c £bn.
Для установления единственности найденной точки докажем методом от противного, что не существует двух различных точек, принадлежащих всем отрезкам системы М одновременно. Пусть два различных числа с¹d (с<d) одновременно принадлежат всем отрезкам системы М: (" nÎN) ®(a n£c£bn)Ù(a n£d£bn).
Из включения [c;d]Ì[ a n;bn] (" nÎN) и условия d-c>0 имеем, что
bn– a n>d–c>0 (" nÎN). Последнее неравенство противоречит определению последовательности стягивающихся отрезков. Нельзя допускать наличия двух различных точек c<d, принадлежащих всем отрезкам системы М. Вывод: остается принять существование одной точки, принадлежащей всем отрезкам стягивающейся системы.n
Рассмотрим числовую последовательность { x n}: x 1, x 2, …, x n ... (2)
Если из последовательности (2) выписывать не все члены подряд, а с пропуском (сохраняя порядок следования), то получаем новую последовательность { 
}: 
, 
, …, , … (3)
Например, можно брать члены с чётными номерами или только с простыми номерами.
Последовательность (3) { }, составленная из членов последовательности (2) с соблюдением порядка следования исходной последовательности, называется подпоследовательностью последовательности (2). При этом:
– член последовательности (2) взятый первым,
k – порядковый номер члена последовательности (3),
nk – номер этого члена в исходной последовательности (2).
В параграфе 1.4 доказано, что всякая сходящаяся последовательность ограничена. Обратное утверждение неверно. Последовательность x n=(-1)n – ограничена, но расходящаяся. Однако, всякая ограниченная последовательность содержит сходящуюся подпоследовательность (например, для xn=(-1)n таковой будет { }: 1,1,1…).
Теорема (Больцано-Вейерштрасс). Из всякой ограниченной последовательности можно выделить сходящуюся к некоторому числу подпоследовательность.
gПо условию { x n} – ограничена, поэтому
($ a,b ÎR):("nÎN)® x nÎ[ a; b ]=D.
Разделим отрезок D пополам. При этом, хотя бы в одной половине, окажется бесконечно много членов последовательности (1) (если в обоих половинах, то условимся брать правую): D1=[ a1;b1 ]ÌD. Выберем один из элементов: ÎD1.
Разделим D1 пополам и снова обозначим через D2 ту половинку, в которой содержится бесконечное число членов x n. Выберем среди них : n2>n1.
Продолжим процесс этот далее. В результате получим последовательность вложенных отрезков Dk=[ ak;bk ] с длинами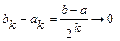 
при k ®¥, а также подпоследовательность { } точек нашей последовательности: ÎDk (n1<n2<…).
Из теоремы о вложенных отрезках существует точка с, принадлежащая любому из отрезков Dk. Очевидно, что { }® с, т.е. с – предел выделенной подпоследовательности.n
