Понятия «множество», «элемент», «принадлежность элемента множеству» - первичные понятия математики. Множество - любое собрание (совокупность) каких- либо предметов.
А является подмножеством множества В, если каждый элемент множества А является элементом множества В, т.е. АÌВ Û (хÎА Þ хÎВ).
Два множества равны, если они состоят из одних и тех же элементов. Речь идет о теоретико-множественном равенстве (не путать с равенством между числами): А=В Û АÌВ Ù ВÌА.
Объединение двух множеств состоит из элементов принадлежащих хотя бы одному из множеств, т.е. хÎАÈВ Û хÎАÚ хÎВ.
Пересечение состоит из всех элементов одновременно принадлежащих как множеству А, так и множеству В: хÎАÇВ Û хÎА Ù хÎВ.
Разность состоит из всех элементов А не принадлежащих В, т.е. хÎ А\В Û хÎА ÙхÏВ.
Декартовым произведением С=А´В множеств А и В называют множество всех возможных пар (х,у), где первый элемент х каждой пары принадлежит А, а второй ее элемент у принадлежит В.
Подмножество F декартова произведения А´В называется отображением множества А в множество В, если выполнено условие: (" х ÎА)($! пара (х.у)ÎF). При этом пишут: А 
В.
Термины «отображение» и «функция» - синонимы. Если ("хÎА)($! уÎВ): (х,у)ÎF, то элемент у Î В называется образом х при отображении F и записывают это так: у =F(х). Элемент х при этом является прообразом (одним из возможных) элемента у.
Рассмотрим множество рациональных чисел Q - множество всех целых чисел и множество всех дробей (положительных и отрицательных). Каждое рациональное число представимо в виде частного, например, 1 
=4/3=8/6=12/9=…. Представлений таких много, но только одно из них несократимо.
В сякое рациональное число можно единственным образом представить в виде дроби p/q, где pÎZ, qÎN, числа p, q- взаимно просты.
Свойства множества Q:
1. Замкнутость относительно арифметических операций. Результат сложения, вычитания, умножения, возведения в натуральную степень, деления (кроме деления на 0) рациональных чисел является рациональным числом: 
; 
; 
.
2. Упорядоченность: ( " х, у ÎQ, х¹у)®(x<y Ú x>y).
Причем: 1) a>b, b>c Þ a>c; 2) a<b Þ -a>-b.
3. Плотность. Между любыми двумя рациональными числами х, у существует третье рациональное число (например, с=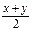 
):
( " х, у ÎQ, x < y)($cÎQ): (х <c< y).
На множестве Q можно выполнять 4 арифметических действия, решать системы линейных уравнений, но квадратные уравнения вида х2=а, аÎ N не всегда разрешимы во множестве Q.
Теорема. Не существует числа хÎQ, квадрат которого равен 2.
g Пусть существует такая дробь х =p/q, где числа p и q взаимно просты и х 2=2. Тогда (p/q)2=2. Следовательно,
p2=2q2. (1)
Правая часть (1) делится на 2, значит p2 четное число. Тем самым р=2n (n-целое). Тогда q должно быть нечетным числом.
Возвращаясь к (1), имеем 4n2=2q2. Поэтому q2=2n2. Аналогично убеждаемся, что q делится на 2, т.е. q - четное число. По методу от противного теорема доказана.n
геометрическое изображение рациональных чисел. Откладывая единичный отрезок от начала координат 1, 2, 3 … раз вправо, получим точки координатной прямой, которые соответствуют натуральным числам. Откладывая аналогично влево, получим точки, соответствующие отрицательным целым числам. Возьмем 1/q (q= 2,3,4 …) часть единичного отрезка и будем откладывать его по обе стороны от начала отсчета р раз. Получаем точки прямой, соответствующие числам вида ±p/q (pÎZ, qÎN). Если p, q пробегают все пары взаимно простых чисел, то на прямой имеем все точки, соответствующие дробным числам. Таким образом, каждому рациональному числу соответствует по принятому способу единственная точка координатной прямой.
Для всякой ли точки можно указать единственное рациональное число? Заполняется ли прямая сплошь рациональными числами?
Оказывается на координатной прямой имеются точки, которым не соответствуют никакие рациональные числа. Строим равнобедренный прямоугольный треугольник на единичном отрезке. Точке N не соответствует рациональное число, так как если ON=x - рационально, то х2= 2, чего не может быть.
Точек, подобных точке N, на прямой бесконечно много. Возьмем рациональные части отрезка х=ON, т.е. 
х. Если отложить их вправо, то каждому из концов любого из таких отрезков не будет соответствовать никакое рациональное число. Допуская, что длина отрезка выражается рациональным числом х= 
, получаем, что х= 
– рационально. Это противоречит доказанному выше.
Рациональных чисел недостаточно, чтобы каждой точке координатной прямой сопоставлять некоторое рациональное число.
Построим множество действительных чисел R через бесконечные десятичные дроби.
По алгоритму деления «уголком» любое рациональное число представимо в виде конечной или бесконечной периодической десятичной дроби. Когда у дроби p/q знаменатель не имеет простых делителей кроме 2 и 5, т.е. q=2m×5k, то результатом будет конечная десятичная дробь p/q=a0,a1a2…an. Остальные дроби могут иметь только бесконечные десятичные разложения.
Зная бесконечную периодическую десятичную дробь, можно найти рациональное число, представлением которого она является. Но любую конечную десятичную дробь можно представить в виде бесконечной десятичной дроби одним из способов:
a0,a1a2…an = a0,a1a2…an 000…=a0,a1a2…(an-1)999… (2)
Например, для бесконечной десятичной дроби х =0,(9) имеем 10 х =9,(9). Если из 10х вычесть исходное число, то получим 9 х =9 или 1=1,(0)=0,(9).
Между множеством всех рациональных чисел и множеством всех бесконечных периодических десятичных дробей устанавливается взаимно однозначное соответствие, если отождествлять бесконечную десятичную дробь с цифрой 9 в периоде с соответствующей бесконечной десятичной дробью с цифрой 0 в периоде по правилу (2).
Условимся употреблять такие бесконечные периодические дроби, которые не имеют цифры 9 в периоде. Если бесконечная периодическая десятичная дробь с цифрой 9 в периоде возникает в процессе рассуждений, то ее будем заменять бесконечной десятичной дробью с нулем в периоде, т.е. вместо 1,999… будем брать 2,000…
Определение иррационального числа. Кроме бесконечных десятичных периодических дробей существуют непериодические десятичные дроби. Например, 0,1010010001… или 27,1234567891011… (после запятой последовательно стоят натуральные числа).
Рассмотрим бесконечную десятичную дробь вида±a0, a1a2…an… (3)
Эта дробь определяется заданием знака «+» или «–», целого неотрицательного числа a0 и последовательности десятичных знаков a1,a2,…,an,…(множество десятичных знаков состоит из десяти чисел: 0, 1, 2,…, 9).
Всякую дробь вида (3) назовем действительным (вещественным) числом. Если перед дробью (3) стоит знак «+», его обычно опускают и пишут a0, a1a2…an… (4)
Число вида (4) будем называть неотрицательным вещественным числом, а в случае, когда хотя бы одно из чисел a0, a1, a2, …, an отлично от нуля, – положительным действительным числом. Если в выражении (3) берется знак «-», то это отрицательное число.
Объединение множеств рациональных и иррациональных чисел образуют множество действительных чисел (QÈJ=R). Если бесконечная десятичная дробь (3) периодическая, то это рациональное число, когда дробь непериодическая – иррациональное.
Два неотрицательных действительных числа а=a0,a1a2…an…, b=b0,b1b2…bn…. называют равными (пишут а=b), если an=bn при n=0,1,2… Число а меньше числа b (пишут a < b), если либо a0<b0, либо a0=b0 и существует такой номер m, что ak=bk (k=0,1,2,…m-1), а am<bm, т.е. a<b Û (a0<b0) Ú ( $ mÎN: ak=bk (k=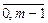 
), am<bm). Аналогично определяется понятие «а > b».
Для сравнения произвольных вещественных чисел введем понятие «модуль числа а». Модулем вещественного числа а=±a0, a1a2…an… называется такое неотрицательное действительное число представимое той же бесконечной десятичной дробью, но взятой со знаком «+», т.е. ½ а ½= a0, a1a2…an… и½ а ½³0. Если а – неотрицательное, b – отрицательное число, то считают а>b. Если оба числа отрицательные (a<0, b<0), то будем считать, что: 1) а=b, если ½ а ½ = ½ b ½; 2) а<b, если ½ а ½ > ½ b ½.
Свойства множества R:
I. Свойства порядка:
1. Для каждой пары действительных чисел а и b имеет место одно и только одно соотношение: a=b, a<b, a>b.
2. Если a<b, b<c, то а<c (транзитивность).
3. Если a<b, то найдется такое число с, что a< с <b.
II. Свойства действий сложения и вычитания:
4. a+b=b+a (коммутативность).
5. (a+b)+c=a+(b+c) (ассоциативность).
6. а+0=а.
7. а+(-а)= 0.
8. из a<b Þ а+с<b+c (" cÎR).
III. Свойства действий умножения и деления:
9. a×b=b×a.
10. (a×b)×c=a×(b×c).
11. а×1=а.
12. а×(1/а)=1 (а¹0).
13. (а+b)×c = ac + bc (дистрибутивность).
14. если a<b и c>0, то а×с<b×c.
IV. Архимедово свойство ("cÎR)($nÎN): (n>c).
Каково бы ни было число сÎR, существует nÎN, что n>c.
V. Свойство непрерывности действительных чисел. Пусть два непустых множества АÌR и BÌR таковы, что любой элемент а ÎА будет не больше (a £ b) любого элемента bÎB. Тогда принцип непрерывности по Дедекинду утверждаетсуществование такого числа с, что для всех а ÎА и bÎB имеет место условие a £c£ b:
(" AÌR, BÌR):(" a ÎA, bÎB ® a £b)($cÎR): (" a ÎA, bÎB® a £c£b).
Будем отождествлять множество R с множеством точек числовой прямой, а вещественные числа называть точками.
