Угловая скорость и угловое ускорение твердого тела, имеющего неподвижную точку.

Примем без доказательства следующую теорему Эйлера: любое перемещение твёрдого тела, имеющего одну неподвижную точку, можно осуществить одним поворотом вокруг оси, проходящей через эту точку. Эта теорема утверждает, что, сколько бы ни делать конечных поворотов, в конечном итоге все эти перемещения эквивалентны одному относительно некоторой оси, проходящей через эту точку. Эту ось назовём осью конечного вращения. Предположим, что тело совершило малый поворот. Введём в рассмотрение вектор малого поворота , равный по величине углу поворота тела и направленный по оси поворота так, чтобы с конца вектора вращение представлялось происходящим против часовой стрелки. Малое перемещение точки М твердого тела с вектор-радиу­сом с точностью до малых высшего порядка опреде­лится вектором . Действительно (рис. 39), величина этого векторного про­изведения равна , т. е. величине перемещения, а направление совпадает с перпендикуляром к плоскости, со­держащей векторы и , в сторону поворота тела.

Пусть тело сначала совершило малый поворот затем также малый поворот ; согласно теореме Эйлера эта сово­купность двух поворотов может быть заменена одним поворо­том с вектором поворота . Чтобы определить этот вектор, возьмем какую-нибудь точку М тела с вектор-радиусом , которая после поворота перейдет в по­ложение М' с вектор-радиусом , при втором повороте точка М' переходит в положение М." с вектор-радиусом

Пренебрегая последним слагаемым, как малым вектором второго порядка, будем иметь

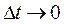Итак, приходим к результату: два последовательных малых поворота тела могут быть заменены одним результирующим вектором поворота, равным геометрической сумме слагаемых векторов поворота; от перемены порядка поворотов результирующий поворот не меняется. Определяя скорость как предел при отношения ма­лого перемещения к промежутку времени , найдем

Вводя вектор угловой скорости 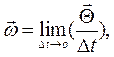получим

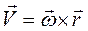(2.24)

Вектор угловой скорости направлен по предельному положению оси того поворота, который тело совершает за рассматриваемый бесконечно малый промежуток времени. Ось эта в отличие от неподвижной оси вращения называется мгновен­ной осью. Что касается величины вектора , то уже нельзя, как раньше, определять ее производной от некоторого угла по вре­мени; при вращении твердого тела вокруг неподвижного центра, так же как и в общем случае пространственного движения твердого тела, такого угла не существует. Иными словами, угловая скорость не является дифферен­циалом некоторого угла.

Покажем, как вычисляется угловая скорость по заданным уравнениям движения тела Для этого заметим, что со­гласно теореме о сложении малых поворотов, всякий ма­лый поворот тела можно представить в виде геометрической суммы трех составляющих поворотов

.

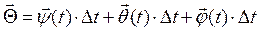Разделив обе части последнего равенства на малый промежуток времени и переходя к пределу, вектор угловой ско­рости этого поворота можно представить в виде суммы трех уг­ловых скоростей составляющих поворота:

Разложим вектор угловой скорости (рис. 36) на оси неподвижной системы координат

Можно записать проекции угловой скорости и на подвижные оси, связанные с вращающимся телом

Из выведенных только что формул следует

. Чтобы получить вектор углового ускорения тела, вращающегося вокруг неподвижной оси, необходимо продифференцировать вектор угловой скорости по времени

,

здесь - орт вектора или орт мгновенной оси вращения; его производная равна , где 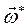- угловая скорость вращения мгновенной оси или вектора угловой скорости. Окончательно имеем

(2.25)

Здесь - характеризует изменение угловой скорости по величине и оно направлено по мгновенной оси вращения, тогда как - характеризует изменение угловой скорости по направлению и оно перпендикулярно мгновенной оси.