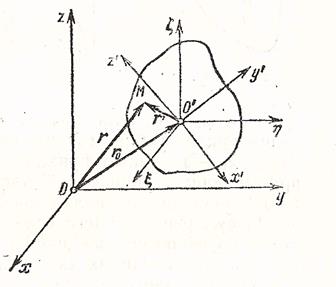
Чтобы определить положение твердого тела в пространстве, зададим прежде всего положение какой-нибудь одной его «основной точки», или полюса О' при помощи вектор-радиуса 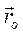 этой точки (рис.40) или ее координат (
этой точки (рис.40) или ее координат (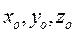 ). Тело может вращаться около фиксированного положения полюса О', поэтому для определения положения тела в пространстве нужно еще задать три эйлеровых угла тела по отношению к системе
). Тело может вращаться около фиксированного положения полюса О', поэтому для определения положения тела в пространстве нужно еще задать три эйлеровых угла тела по отношению к системе 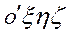 , оси которой параллельны неподвижым осям Охуz, а начало находится в полюсе О. Так, твердое тело в пространстве имеет шесть степеней свободы, характеризуемых величинами
, оси которой параллельны неподвижым осям Охуz, а начало находится в полюсе О. Так, твердое тело в пространстве имеет шесть степеней свободы, характеризуемых величинами
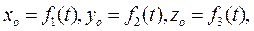
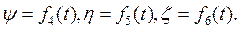 Имея заданными эти шесть величин, легко составить и уравнения движения любой точки М тела. Из основного равенства
Имея заданными эти шесть величин, легко составить и уравнения движения любой точки М тела. Из основного равенства 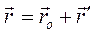 ,проектированием его на оси неподвижной системы координат получим
,проектированием его на оси неподвижной системы координат получим
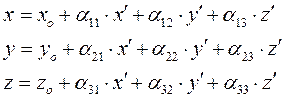 (2.29)
(2.29)
|
| Рис 40 |
Здесь  - направляющие косинусы- (обозначения их приняты согласно таблице, помещенной в предыдущем параграфе) могут быть выражены через эйлеровы углы; величины х', у', z' — заданные постоянные, определяющие выбор точки, движение которой разыскивается,
- направляющие косинусы- (обозначения их приняты согласно таблице, помещенной в предыдущем параграфе) могут быть выражены через эйлеровы углы; величины х', у', z' — заданные постоянные, определяющие выбор точки, движение которой разыскивается, 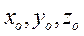 - заданные функции времени. Таким образом, уравнения (2.29) дают уравнения движения точек тела.
- заданные функции времени. Таким образом, уравнения (2.29) дают уравнения движения точек тела.
Всякое перемещение тела в пространстве может быть, осуществлено поступательным перемещением вместе с полюсом и одним поворотом вокруг оси, проходящей через полюс.
В дополнение к вышесказанному добавим, что вектор поворота тела не зависит от выбора полюса, т. е. при перемене полюса будет меняться только поступательное перемещение, а ось, угол и направление поворота не будут изменяться.
Скорости и ускорения в общем случае движения
Твердого тела.
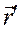 Перемещение любой точки тела, как было показано, складывается из поступательного перемещения, равного перемещению полюса, и вращательного вокруг оси, проходящей через полюс. Если рассматривать только бесконечно малые перемещения тела, соответствующие переходу тела из данного положения в бесконечно близкое, то с точностью до бесконечно малых высших порядков можно представить вращательное перемещение как векторное произведение вектора бесконечно малого поворота
Перемещение любой точки тела, как было показано, складывается из поступательного перемещения, равного перемещению полюса, и вращательного вокруг оси, проходящей через полюс. Если рассматривать только бесконечно малые перемещения тела, соответствующие переходу тела из данного положения в бесконечно близкое, то с точностью до бесконечно малых высших порядков можно представить вращательное перемещение как векторное произведение вектора бесконечно малого поворота 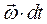 на вектор-радиус рассматриваемой точки по отношению к полюсу.
на вектор-радиус рассматриваемой точки по отношению к полюсу.
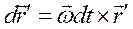 .
. 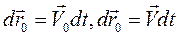
Так как 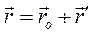 , то
, то 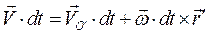 , где
, где  -скорость полюса, разделив полученное выражение на
-скорость полюса, разделив полученное выражение на 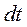 , получим
, получим
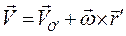 . (2.30)
. (2.30)
Эта основная формула кинематики твердого тела дает закон распределения скоростей в твердом теле в общем случае его движения.
Слагаемое 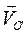 определяет поступательную составляющую скорости, равную скорости полюса, второе слагаемое представляет собой вращательную составляющую скорости тела вокруг полюса О'.
определяет поступательную составляющую скорости, равную скорости полюса, второе слагаемое представляет собой вращательную составляющую скорости тела вокруг полюса О'.
Зная движение полюса и закон вращения тела вокруг полюса, т. е. имея уравнения движения, можем по формуле (2.30) определить скорость любой точки тела. Проекции скорости на оси получим по общим правилам проектирования векторных выражений. Выпишем проекции скорости на неподвижные оси:
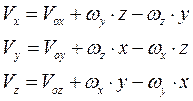
Здесь 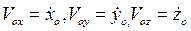 Переходим к рассмотрению вопроса о распределении ускорений. Для этого продифференцируем левую и правую части (49) по времени; получим
Переходим к рассмотрению вопроса о распределении ускорений. Для этого продифференцируем левую и правую части (49) по времени; получим
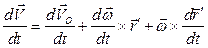
или
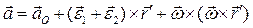 (2.31)
(2.31)
Первое слагаемое 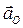 определяет поступательное ускорение, равное ускорению полюса, а второе и третье:
определяет поступательное ускорение, равное ускорению полюса, а второе и третье: 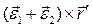 и
и 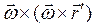 - вращательную и центростремительную составляющие ускорения вращения тела вокруг полюса. Таким образом, получаем: ускорение точки твердого тела в общем случае его движения складывается из трех составляющих: 1) поступательного ускорения, одинакового в данный момент для всех точек тела и равного ускорению полюса; 2) вращательного ускорения вокруг полюса (
- вращательную и центростремительную составляющие ускорения вращения тела вокруг полюса. Таким образом, получаем: ускорение точки твердого тела в общем случае его движения складывается из трех составляющих: 1) поступательного ускорения, одинакового в данный момент для всех точек тела и равного ускорению полюса; 2) вращательного ускорения вокруг полюса (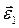 направлено по мгновенной оси и характеризует изменение угловой скорости по величине,
направлено по мгновенной оси и характеризует изменение угловой скорости по величине, 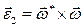 - характеризует изменение угловой скорости по направлению и оно перпендикулярно мгновенной оси), 3) осестремительного ускорения, равного по величине произведению квадрата угловой скорости на кратчайшее расстояние от точки до мгновенной оси вращения.
- характеризует изменение угловой скорости по направлению и оно перпендикулярно мгновенной оси), 3) осестремительного ускорения, равного по величине произведению квадрата угловой скорости на кратчайшее расстояние от точки до мгновенной оси вращения.
Глава 8.






