Общая постановка задачи об относительном движении такова: движение точки определяется наблюдателями, связанными с двумя различными координатными системами (системами отсчета), причем эти системы движутся заданным образом друг по отношению к другу. Каждый наблюдатель определяет кинематические элементы движения: траекторию, скорость и ускорение в своей системе отсчета. Ставится задача: зная движение одной системы отсчета по отношению к другой, найти связь между кинематическими элементами движения точки по отношению к каждой системе в отдельности. Предположим, что движение точки М в пространстве рассматривается в двух движущихся друг по отношению к другу системах координат: Oxyz, и 
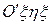(рис.41). В зависимости от содержания стоящей перед нами задачи одну из этих систем Oxyz примем за основную и назовем абсолютной системой и все кинематические элементы его абсолютными. Другую систему 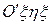назовем относительной и соответственно движение по отношению к этой системе, а также его кинематические элементы относительными. Термины «абсолютный» и «относительный» имеют здесь условное значение; при рассмотрении движений может оказаться целесообразным то одну, то другую систему принимать за абсолютную. Элементы абсолютного движения будем обозначать подстрочным индексом «а», а относительного — индексом «r».
Введем понятие переносного движения, элементы которого будем обозначать подстрочным индексом «е». Переносным движением точки будем называть движение (по отношению к абсолютной системе) того пункта относительной системы, через который в рассматриваемый момент времени проходит движущаяся точка. Понятие переносного движения нуждается в пояснении. Необходимо четко различать точку, абсолютное и относительное движение которой рассматривается, от той, неизменно связанной с относительной системой точки, через которую в данный момент проходит движущаяся точка. Обычно та и другая точка обозначены одной буквой М, так как рисунок не передает движения; на самом деле это две различные точки, движущиеся друг по отношению к другу.
Остановимся на двух иллюстрациях понятия переносного движения. Если человек идет по движущейся платформе, то можно рассматривать, во-первых, «абсолютное» движение человека по отношению к земле, во-вторых, «относительное» его движение по платформе. Переносным движением при этом будет являться движение по отношению к земле того места платформы, по которому проходит в данный момент человек.
Возвращаясь к рис. 41, найдем зависимость между вектор-радиусами точки М в разных системах координат. Если обозначить вектор-радиусы точки М через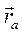 
в абсолютной системе Oxyz и 
в относительной системе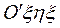 
, а вектор-радиус точки О' по отношению к системе Oxyz через 
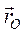, то
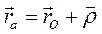(2.32)
Принципиальное отличие равенств (2.32) от имеющих тот же внешний вид уравнений движения твердого тела заключается в том, что в выражении (2.32) уже не постоянный вектор, определяющие выбор точки твердого тела, а вектор-функция времени, характеризующий относительное движение точки М.
