Способы задания движения точки. Уравнения движения точки; траектория.

КИНЕМАТИКА

__________________________________________________________

В разделе кинематики мы изучаем движение и устанавливаем основные пространственно – временные характеристики движения. В настоящем разделе, посвященном кинематике, отвлекаются от силовых взаимодействий между материальными телами и влияния на них силовых полей, а рассматривают механические движения тел, в отрыве от причин, которые создают и поддерживают эти движения. Движения в кинематике изучаются по отношению к некоторой системе отсчёта, представляющей жесткую, неограниченно простирающуюся во все стороны систему точек. В кинематике неважно, движется ли эта система или принимается неподвижной. Отметим, что такое равноправие систем не имеет места в динамике. В этом пространстве выбирается тело отсчёта, а в нём систему координат, например, три взаимно перпендикулярные координатные оси, служащие для определения положения отдельных точек тел.

Как указывалось в начале, пространство рассматривается как евклидово, так, применение теоремы Пифагора позволяет определить квадрат расстояния между двумя точками как сумму квадратов разностей соответствующих координат точек и т. п. Наряду с абсолютным пространством в классической кинематике используется понятие «абсолютного времени», одинаково и равномерно текущего во всех точках абсолютного пространства. В качестве такого времени принимается звёздное или среднее солнечное время. Заметим, что все выводы классической механики с достаточной для практики точностью справедливы, если скорости движения малы по сравнению со скоростью распространения света, а размеры областей пространства, в которых происходит движение, далеки от космических расстояний.

 

 

Глава 4.

 

Кинематика точки.

Способы задания движения точки. Уравнения движения точки; траектория.

1. Координатный способ задания положения и движения точки. Положение точки в пространстве (рис. 17) будем определять ее вектор-радиусом , проведенным из произвольной, выбранной наперед точки О (начала коор­динатной системы Oxyz). Из представленного рисунка (рис. 17) сразу видно, что проек­ции вектор-радиуса точки М на оси декартовых координат представляют не что иное, как координаты точки. Применяют и другие способы определения положения точки. Так, например, пользуются сферическими координатами: расстоянием r точки М от точки О (рис. 17), углом φ, и углом θ между осью OZ и вектор-радиусом . Вместо последнего угла θ можно рассматривать дополнительный угол ψ наклона вектор-радиуса к плоскости ОXY.

Координаты эти носят различные наименования в зависимости от области применения. Угол φ называют азимутом, иногда долготой, угол ψ - широтой, угол θ - полюсным углом. Если точка M лежит в плоскости Оху, то координаты φ и ρ носят наименование полярных координат. Для определения положения точки в пространстве существуют и другие системы координат, называемые вообще криволинейными координатами. Приведем формулы связи между декартовыми, цилиндрическими и сферическими координатами точки. Из рис. 17 следует:

х= ρ соsφ = r sin θ cos φ= r cos ψсоsφ,

у =ρ sin φ = r sin θ sin φ = r cos ψ sin φ, (2.1)

z = r cos θ = r sin ψ.

Если точка движется в пространстве, то ее координаты изме­няются с течением времени. По закону изменения этих координат можно судить о характере движения точки. Предположим, что нам заданы координаты точки в функции времени, т. е. заданы уравнения

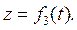
Эти уравнения называются уравнениями движения точки в де­картовых координатах. Вместо декартовых координат х, у, z можно взять какие угодно другие координаты: полярные, сферические, цилиндрические и др. Выраженные в функции времени, они дадут уравнения движения точки в соответствующей системе координат.

2. Естественный способ задания точки.

Линия, описываемая движущейся точкой в пространстве, назы­вается траекторией. Для получения уравнений траекто­рии необходимо из уравнений движения исключить время. При естественном способе задания движения точки задаётся траектория движения точки и дуга S(t), отсчитываемая от выбранного начала до положения точки на траектории. Можно представить траекторию движения как дорогу, по которой идёт человек, а S(t) как расстояние, пройденное по этой дороге.