Под полным исследованием функции обычно понимается решение таких вопросов:
- Определение области существования функции.
- Выявление вопроса о четности и нечетности функции.
- Определение точек разрыва функции.
- Определение асимптот графика функции.
- Определение интервалов возрастания и убывания функции.
- Определение экстремума функции.
- Определение интервалов выпуклости и вогнутости графика функции.
- Определение точек перегиба.
- Нахождение пересечения с осями координат.
- Построение графика функции.
Пример. Исследуем функцию 
D (y) = ( ). Функция непрерывна на всей области определения. Точек разрыва нет.
). Функция непрерывна на всей области определения. Точек разрыва нет.
Функция не является ни четной, ни нечетной, ни периодической.
Точек разрыва нет.
Вертикальных асимптот нет;  , наклонных асимптот нет.
, наклонных асимптот нет.
5, 6. 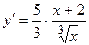 . Критические точки х = -2, х = 0.
. Критические точки х = -2, х = 0.
| х | (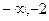 ) )
| -2 | (-2, 0) | ( ) )
| |
Знак 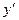
| + | 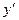 = 0 = 0
| - | 
| + |
| Поведение функции | Возрастает | max
3 
| Убывает | min | Возрастает |
7, 8.  ,
,  при х = 1,
при х = 1,  не существует при х = 0.
не существует при х = 0.
| х | ( ) )
| (0, 1) | ( ) )
| ||
Знак 
| - |  = = 
| - |  = 0 = 0
| + |
| Поведение функции | Выпукла верх | Не является точкой перегиба | Выпукла верх | Точка перегиба у = 6 | Выпукла вниз |
9. 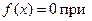 х =0 и х = -5.
х =0 и х = -5.
10.

Задание 1
1. Вычислить определитель матрицы А второго порядка
2. Вычислить определитель матрицы В третьего порядка
3. Вычислить определитель матрицы В, разложив его по какой-либо строке и какому либо столбцу
4. Вычислить определитель матрицы В, пользуясь свойствами определителей. Свести вычисление определителя третьего порядка к вычислению одного определителя второго порядка
| Вариант 1 | ||||||||||||||||
| A = | ( | -3 | -6 | ) | B = | ( | -1 | ) | ||||||||
| -5 | ||||||||||||||||
| -2 | -4 | |||||||||||||||
| Вариант 2 | ||||||||||||||||
| A = | ( | ) | B = | ( | -1 | -4 | -4 | ) | ||||||||
| -9 | -3 | -4 | -1 | |||||||||||||
| -1 | -2 | |||||||||||||||
| Вариант 3 | ||||||||||||||||
| A = | ( | -1 | ) | B = | ( | -5 | -3 | ) | ||||||||
| -1 | -8 | -4 | -4 | |||||||||||||
| -3 | -1 | |||||||||||||||
| Вариант 4 | ||||||||||||||||
| A = | ( | -10 | -7 | ) | B = | ( | -1 | -2 | ) | |||||||
| -3 | ||||||||||||||||
| -5 | -5 | |||||||||||||||
| Вариант 5 | ||||||||||||||||
| A = | ( | ) | B = | ( | -4 | -4 | -1 | ) | ||||||||
| -5 | -1 | -3 | ||||||||||||||
| -5 | ||||||||||||||||
| Вариант 6 | ||||||||||||||||
| A = | ( | -8 | -1 | ) | B = | ( | ) | |||||||||
| -3 | -2 | -4 | ||||||||||||||
| -4 | -3 | |||||||||||||||
| Вариант 7 | ||||||||||||||||
| A = | ( | -8 | ) | B = | ( | -3 | -1 | ) | ||||||||
| -9 | -8 | -2 | ||||||||||||||
| -2 | -1 | |||||||||||||||
| Вариант 8 | |||||||||||
| A = | ( | -6 | ) | B = | ( | -4 | ) | ||||
| -1 | -1 | -1 | |||||||||
| -4 | -3 | ||||||||||
| Вариант 9 | |||||||||||
| A = | ( | -2 | ) | B = | ( | -2 | ) | ||||
| -5 | -4 | -1 | |||||||||
| Вариант 10 | |||||||||||
| A = | ( | -4 | -9 | ) | B = | ( | -1 | -5 | ) | ||
| -5 | -3 | -5 | |||||||||
| -2 | -4 |
Задание 2
1. Решить методом Крамера систему уравнений Ах = а
2. Решить методом Крамера систему уравнений Вx = b
3. Решить методом Гаусса систему уравнений Вx = b
| Вариант | ||||||||||||||||||
| B = | ( | -3 | ) | b= | ( | ) | ||||||||||||
| A = | ( | ) | a= | ( | -5 | ) | -1 | -8 | ||||||||||
| -1 | -2 | -1 | -3 | |||||||||||||||
| Вариант | ||||||||||||||||||
| B = | ( | -4 | -3 | ) | b= | ( | ) | |||||||||||
| A = | ( | ) | a= | ( | ) | -1 | -5 | |||||||||||
| -4 | -2 | -6 | -2 | -9 | ||||||||||||||
| Вариант | ||||||||||||||||||
| B = | ( | -4 | ) | b= | ( | -5 | ) | |||||||||||
| A = | ( | -4 | -1 | ) | a= | ( | -1 | ) | -1 | -2 | ||||||||
| -1 | -3 | -3 | -3 | -2 | -1 | |||||||||||||
| Вариант | ||||||||||||||||||
| B = | ( | -5 | -4 | ) | b= | ( | ) | |||||||||||
| A = | ( | -2 | -3 | ) | a= | ( | -5 | ) | -2 | |||||||||
| -4 | -16 | -3 | ||||||||||||||||
| Вариант | ||||||||||||||||||
| B = | ( | -1 | -5 | ) | b= | ( | ) | |||||||||||
| A = | ( | -5 | ) | a= | ( | ) | -2 | -3 | ||||||||||
| -4 | -5 | -4 | -3 | |||||||||||||||
| Вариант | ||||||||||||||||||
| B = | ( | -1 | -5 | ) | b= | ( | ) | |||||||||||
| A = | ( | ) | a= | ( | ) | -3 | ||||||||||||
| -1 | -9 | -4 | ||||||||||||||||
| Вариант | ||||||||||||||||||
| B = | ( | -2 | -1 | ) | b= | ( | -8 | ) | ||||||||||
| A = | ( | -5 | ) | a= | ( | -5 | ) | -3 | -4 | |||||||||
| -5 | -4 | |||||||||||||||||
| Вариант | ||||||||||||||||||
| B = | ( | -2 | ) | b= | ( | ) | ||||||||||||
| A = | ( | -3 | -2 | ) | a= | ( | -1 | ) | -4 | |||||||||
| -4 | -5 | -1 | ||||||||||||||||
| Вариант | ||||||||||||||||||
| B = | ( | -3 | -2 | ) | b= | ( | -11 | ) | ||||||||||
| A = | ( | -1 | -4 | ) | a= | ( | ) | -4 | -5 | -14 | ||||||||
| -1 | -1 | -5 | -10 | |||||||||||||||
| Вариант | ||||||||||||||||||
| B = | ( | -3 | ) | b= | ( | -5 | ) | |||||||||||
| A = | ( | ) | a= | ( | -14 | ) | -5 | -1 | ||||||||||
| -1 | -7 | -2 | -1 | |||||||||||||||
Задание 3.
1. Решить матричным методом систему уравнений Ах = а
2. Решить матричным методом систему уравнений Вx = b
| Вариант | |||||||||||||||||||
| B = | ( | -3 | ) | b= | ( | ) | |||||||||||||
| A = | ( | -1 | ) | a= | ( | ) | -2 | -12 | |||||||||||
| -3 | -2 | ||||||||||||||||||
| Вариант | |||||||||||||||||||
| B = | ( | -1 | ) | b= | ( | ) | |||||||||||||
| A = | ( | -5 | -3 | ) | a= | ( | ) | -2 | -4 | ||||||||||
| -2 | -5 | -1 | -13 | ||||||||||||||||
| Вариант | |||||||||||||||||||
| B = | ( | -3 | -3 | ) | b= | ( | -6 | ) | |||||||||||
| A = | ( | -3 | -5 | ) | a= | ( | ) | -1 | |||||||||||
| -6 | -4 | -5 | -3 | ||||||||||||||||
| Вариант | |||||||||||||||||||
| B = | ( | -3 | -5 | ) | b= | ( | ) | ||||||||||||
| A = | ( | -1 | ) | a= | ( | -1 | ) | -1 | -2 | ||||||||||
| -5 | -5 | -2 | -2 | -5 | |||||||||||||||
| Вариант | |||||||||||||||||||
| B = | ( | ) | b= | ( | -5 | ) | |||||||||||||
| A = | ( | ) | a= | ( | -3 | ) | -5 | -3 | -1 | ||||||||||
| -2 | -2 | -7 | |||||||||||||||||
| Вариант | |||||||||||||||||||
| B = | ( | -3 | ) | b= | ( | -6 | ) | ||||||||||||
| A = | ( | -2 | ) | a= | ( | ) | -4 | -3 | |||||||||||
| -4 | -6 | -5 | |||||||||||||||||
| Вариант | |||||||||||||||||||
| B = | ( | -3 | -2 | ) | b= | ( | ) | ||||||||||||
| A = | ( | -4 | -4 | ) | a= | ( | -4 | ) | -4 | -5 | -5 | ||||||||
| -5 | -5 | -2 | -2 | ||||||||||||||||
| Вариант | |||||||||||||||||||
| B = | ( | -4 | ) | b= | ( | ) | |||||||||||||
| A = | ( | -2 | ) | a= | ( | -21 | ) | -3 | |||||||||||
| -2 | -11 | -3 | -4 | ||||||||||||||||
| Вариант | |||||||||||||||||||
| B = | ( | -3 | ) | b= | ( | -15 | ) | ||||||||||||
| A = | ( | ) | a= | ( | -4 | ) | -3 | -16 | |||||||||||
| -1 | -1 | -5 | |||||||||||||||||
| Вариант | |||||||||||||||||||
| B = | ( | -3 | ) | b= | ( | -2 | ) | ||||||||||||
| A = | ( | -1 | ) | a= | ( | -7 | ) | -2 | |||||||||||
| -5 | -3 | -2 | -2 |
Задание 4.
Вычислить ранг матрицы.
1.  , 2.
, 2.  ;
;
3.  4.
4. 
5.  6.
6. 
7.  8
8 
9.  10.
10. 
Задание 5
Даны две вершины треугольника Δ АВС: А (х1,у1), В (х2,у2) и точка D (x3,y3)пересечения высот:
а) составить уравнение высот, медиан, биссектрис треугольника Δ АВС.
б) найти уравнения прямых, проходящих через вершины треугольника и параллельных сторонам.
в) определить длины высот треугольника и расстояние от точки М (х4, у4) до сторон треугольника.
| n | x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 |
| 1. | ||||||||
| 2. | ||||||||
| 3. | ||||||||
| 4. | ||||||||
| 5. | -2 | |||||||
| 6. | ||||||||
| 7. | ||||||||
| 8. | ||||||||
| 9. | ||||||||
| 10. | -3 |
Задание 6.
Даны координаты вершин пирамиды АВСD: А (х1,у1,z1), В (х2,у2,z3), C (x2,y2,z2), D (х4, у4,z3)
Найти:
1) длину ребра АВ;.
2) угол между ребрами АВ и АD;
3) угол меду ребром AD и гранью ABC;
4) площадь грани ABC;
5) объем пирамиды;
6) уравнение прямой AB;
7) уравнение плоскости ABC;
8) уравнение высоты, опущенной из вершины D на грань ABC.
| n | x1 | y1 | z1 | x2 | y2 | z2 | x3 | y3 | z3 | x4 | y4 | z4 |
| 1. | -5 | |||||||||||
| 2. | -1 | |||||||||||
| 3. | -5 | -3 | ||||||||||
| 4. | -2 | -3 | -1 | |||||||||
| 5. | -6 | -6 | ||||||||||
| 6. | -1 | |||||||||||
| 7. | -3 | -5 | -4 | |||||||||
| 8. | -2 | -3 | -1 | |||||||||
| 9. | -12 | |||||||||||
| 10. | -3 | -6 |
Задание 7.
1. Составить уравнение линии, для каждой точки которой отношений расстояние до точки А (3,0) и до прямой х = 12 равно ε = 0,5 полученное уравнение привести к простейшему виду и построить прямую.
2. Составить уравнение линии, для каждой точки которой отношений расстояние до точки А (-3,4) равно расстоянию до прямой у = 2. Полученное уравнение привести к простейшему виду и построить прямую.
3. Показать, что  есть уравнение окружности. Найти ее центр и радиус.
есть уравнение окружности. Найти ее центр и радиус.
4. Написать уравнение окружности, проходящей через точки: (0,1), (2,0), (3,1).
5. Гипербола проходит через точки (3,  ) и (
) и (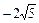 ,3). Найти уравнение гиперболы.
,3). Найти уравнение гиперболы.
6. Найти уравнение асимптот гиперболы  .
.
7. Найти острый угол между асимптотами гиперболы, если ее эксцентриситет равен 2.
8. Дана равнофокусная гипербола  . Найти уравнение эллипса, фокусы которого находится в фокусах гиперболы, если известно, что эллипс проходит через точку А (4,6).
. Найти уравнение эллипса, фокусы которого находится в фокусах гиперболы, если известно, что эллипс проходит через точку А (4,6).
9. Составить уравнение параболы, зная, что вершина ее находится в начале координат и расстояние от фокуса до вершины равно 4 единицам длины, а осью симметрии служит ось Ох.
10. Парабола симметрична относительно оси Ох, проходит через точку А (4,-1), а вершина ее лежит в начале координат. составить ее уравнение.
Задание 8. Найти область определения функции
1. 
2. 
3. 
4. 
5. 
6. 
7. 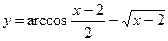
8. 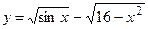
9. 
10. 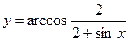
Задание 9.Построить график функции
1. 
2. 
3. 
4 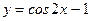
5. 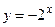
6. 
7. 
8. 
9. 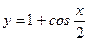
10. 
Задание 10.Найти пределы функции
1.а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д) 
2.а)  , б)
, б) 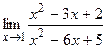 , в)
, в)  ,
,
г)  , д)
, д) 
3.а)  , б)
, б)  , в)
, в) 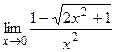 ,
,
г) 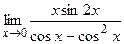 , д)
, д) 
4. а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д) 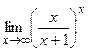
5.а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д) 
6.а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д) 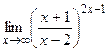
7. а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д) 
8.а)  , б)
, б)  , в)
, в)  ,
,
г) 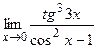 , д)
, д) 
9.а)  , б)
, б)  , в)
, в) 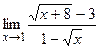 ,
,
г)  , д)
, д) 
10.а) 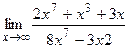 , б)
, б) 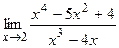 , в)
, в)  ,
,
г)  , д)
, д) 
Задание 11. Найти производную
1.  , б)
, б)  ,
,
в)  , г)
, г) 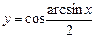 , д)
, д)  , е)
, е) 
2. а)  , б)
, б) 






